Supervised Learning of Behaviors
这一节还未涉及到强化学习,仅仅是讨论用于学习策略的监督学习方式
Terminology and Notation
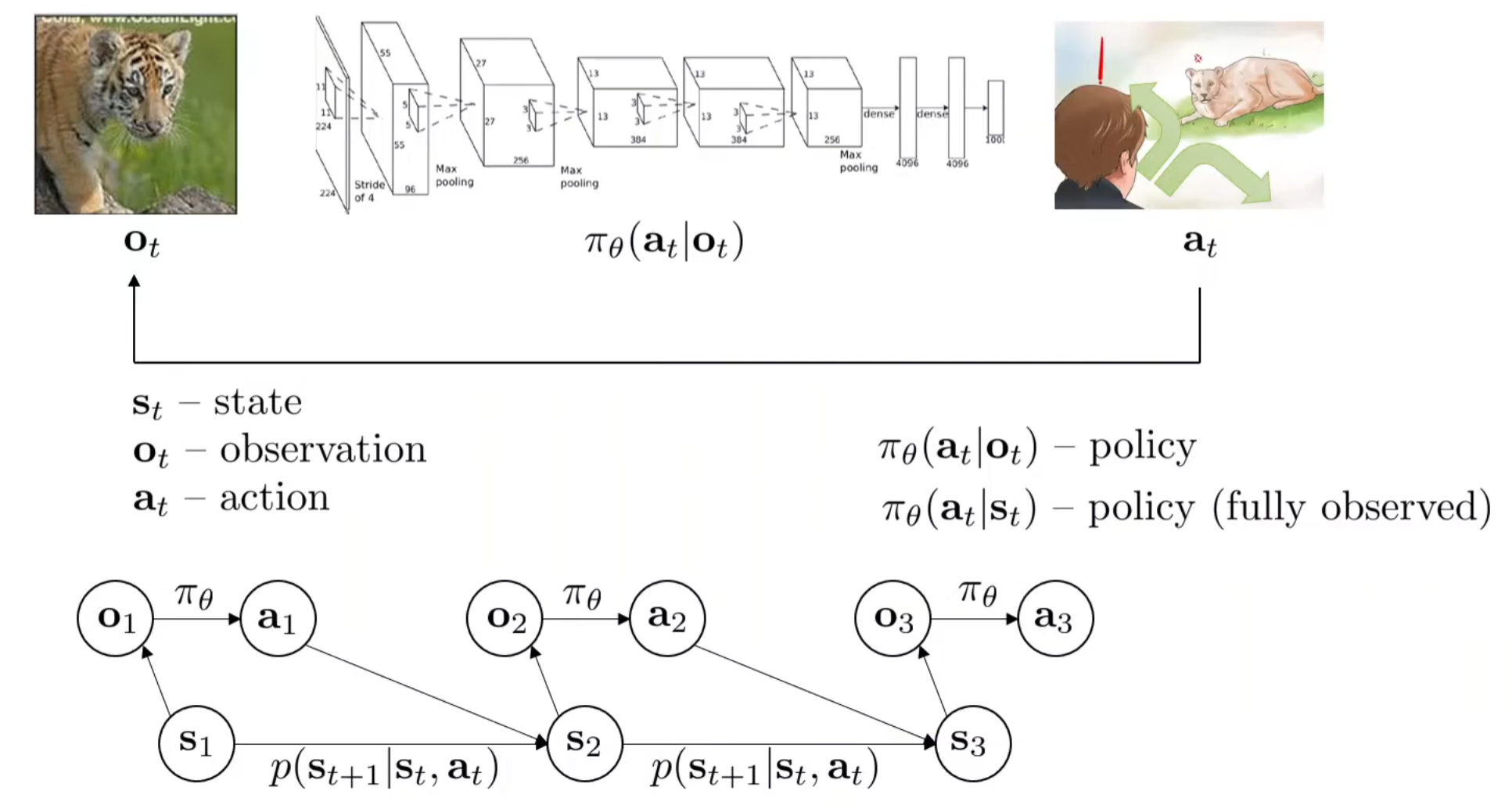
首先定义策略:在一定观察下,做出对应的行动。因此有\(\mathbf{o}_t \ \mathbf{a}_t\),其中前者为observation观察,后者为action,下标t代表的是第t时间步。当然时间是连续的情况下,\(\delta t\)会非常短。用\(\pi\)代表policy策略,\(\theta\)代表策略里面的参数,因此在t时间步给定观察后做出反应的策略为:
在控制理论中,state常用\(x\),action常用\(u\),这个notation来自苏联科学家
值得注意的是,\(\mathbf{a}\)在离散的行动选项空间代表的是概率分布,而在连续的行动选项空间中代表的是连续概率分布。虽然我们其实可能只想要选出一个action,但是得到分布然后choose accordingly是Intuitive的。
与observation非常相似但是实则区别很多的一个概念是state。state and observation的关系可以用CS181(CS188)中的HMM中的二者关系来近似理解。一般认为对应的state影响observation,但是在这个例子中,还引入了一个action因素,它也会影响下一个时间点的state。因此,贝叶斯网络如图所示。其中当前时间步的action纯粹由当前的观察得出,并且下一时间步的state是收到上一时间步的状态和行动影响的,故state的transition为:
Behavioral Cloning
Why working not well?
在监督学习中,给定input输出output是它最熟悉的任务,因此在此情境中,监督学习策略就是在人类提供的大量\((o_t,a_t)\)数据下进行拟合。比如说在自动驾驶的简单场景中,就是给定车前面摄像头的图像,然后决定左转、右转还是直走。这种训练的范式就是监督学习,来学习policy,有时也叫做behavioral cloning,因为我们希望模型网络能够‘克隆’人类的操作。
这种paradigm work吗?实践证明:不是很work!以下图为例子进行直观上的感受:
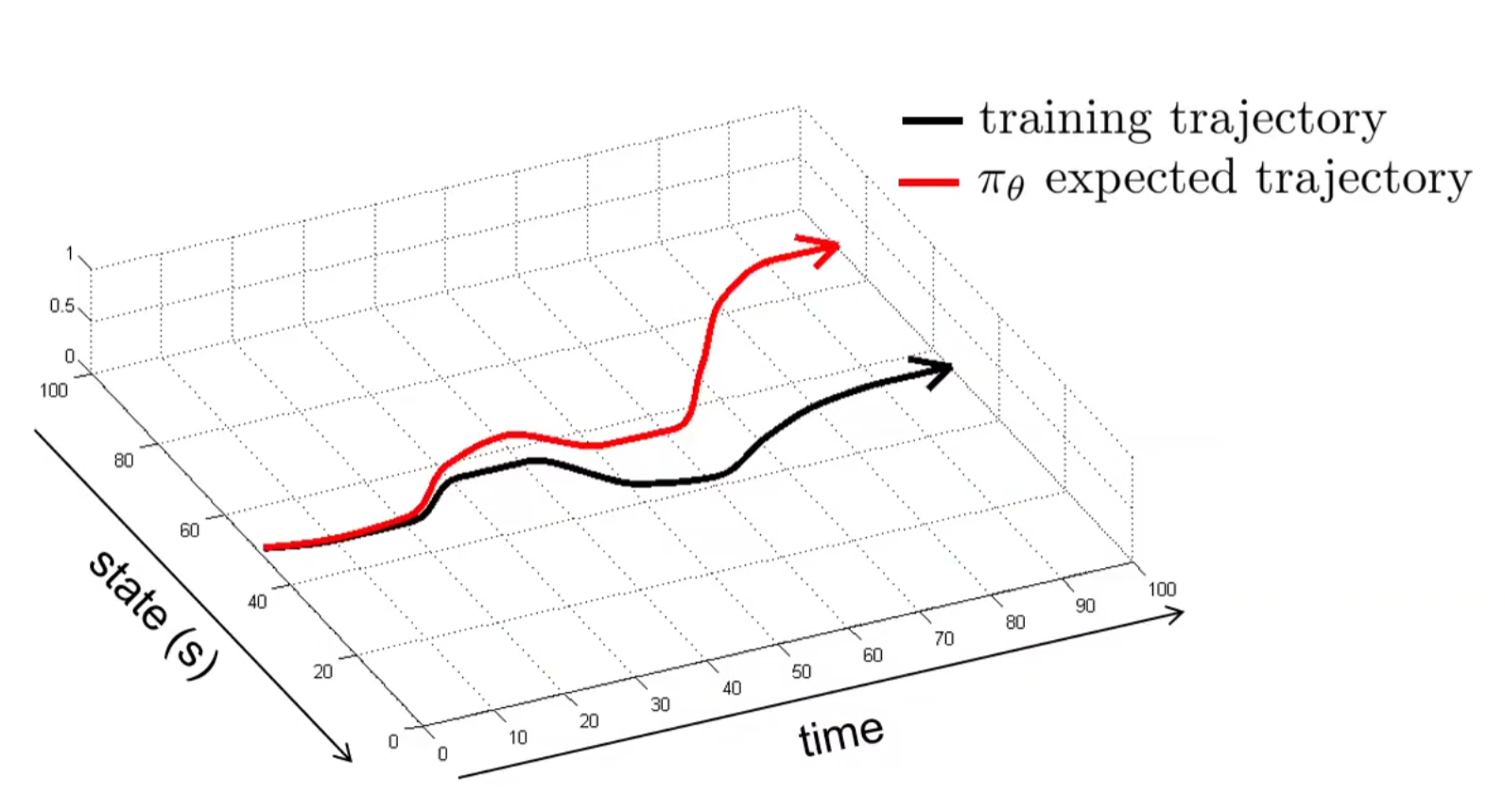
假设训练的轨迹如图中黑色,然后我们开始进行inference。假设开始的20个时间步表现的很好,但是网络输出总是有错的时候,那么假设20步之后开始犯下错误。当犯下错误之后,进入的状态是训练集中从来没见到过的场景!比如说开车的例子中,人类的开始在直线道路上都是直走的,如果模型推理的时候左打了一些方向,那么车的轨迹歪掉了,之后的图像中的车道都是斜着的,模型就不认识了,但是人类是知道往右打方向盘来纠正的!根据上述的论述,因此模型的表现在出现错误之后就很难纠正回来,直至大错特错。
Imitation learning via behavioral cloning is not guaranteed to work!更进一步地,其不work的原因在于:i.i.d assumption does not hold。模型学出来的,严格来说,是\(\pi_\theta(\mathbf{a}|\mathbf{o})\)而不是\(\pi_\theta(\mathbf{a}_t|\mathbf{o}_t)\),因此每一个时间点的policy其实是完全独立的!但是正如之前介绍贝叶斯网络中所提及的,下一时间步的state是收到上一时间步的状态和行动影响的,但是模仿学习并没有建模time step,state的。
我们可以用理论的方式来更为规范地证明模仿学习不work。假设数据集\(o_t\)的分布是\(p_{data}(o_t)\),然后有对应的\(a_t\),那么很intuitively,我们可能设计训练目标:优化参数\(\theta\)来最大化似然。这在机器学习中很常见。 然后假设训练(inference)的时候,observation的分布换成了\(p_{\pi \theta}(o_t)\),很显然,有相当高的概率:\(p_{data}(o_t)\neq p_{\pi \theta}(o_t)\)。但是这样的训练目标真的好吗?最大化似然将会使得policy在相似的observation下对人类当初的action有着较高的概率,但是在稍微不同的observation下采取完全不同的行动。因此训练的时候,我们考虑修改优化目标: 在训练的过程中,每错一步就要付出一个单位的成本,而目标就是最小化错误成本(假设人类驾驶员的policy是consistent的)。因此目标是:
Minimize the number of mistakes the policy makes when we run it.
假设最终我们训练出来的模型满足:\(\pi_{\theta}(a \neq \pi^{\star}(s)|s)≤\epsilon\),即犯错的概率小于epsilon,那么我们考虑在t步中的犯错期望数为:
第一项:第一步就错,那么之后的步骤就都错掉了;如果不错,考虑第二步,递归下去...
上述推导了在最坏的情况下,犯错次数是\(O(T^2)\)的。我们也可以推导:事实上行为克隆的表现不会比这个复杂度差。
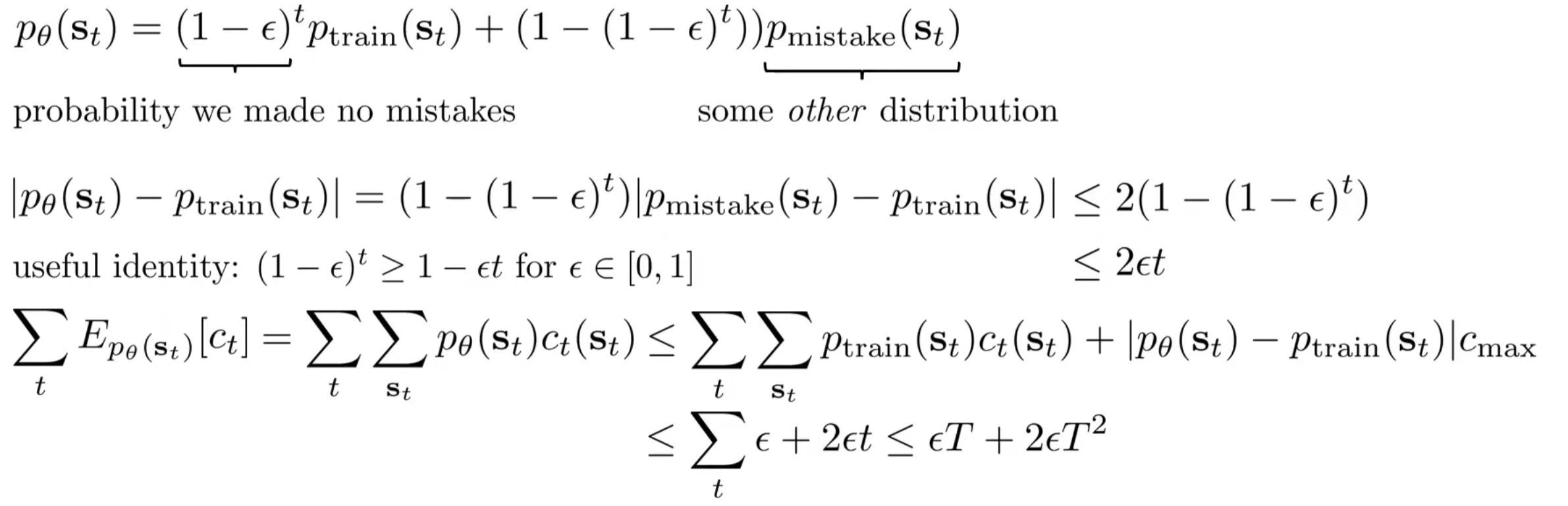
在上面的推导中,首先提出:在测试的时候,\(s_t\)的分布和训练时的是有差别的,且假设我们不是很清楚\(p_{mistake}\)。然后进行简单的概率分布绝对值放缩和基于欧拉展开的放缩,对最后的期望式子改写出放缩项,最后得出一般情况下的错误次数上界。\(O(T^2)\)的错误次数数量级很是令人沮丧。
key insight:如果\(p_{train}\)的范围很广呢?那么是不是将会尽可能地满足\(p_{train}(o_t)\approx p_{\pi \theta}(o_t)\)呢?而如果要满足这一点,是不是数据集里面不能全都是‘正确’的样本,也需要记录一下错误并且修正的样本呢?事实上就是如此:越完美的数据集,训练出来的policy越不robust,因为一旦错误进入到训练集中没见过的场景中,模型便不知道如何做出correction action了。
Addressing the problem!
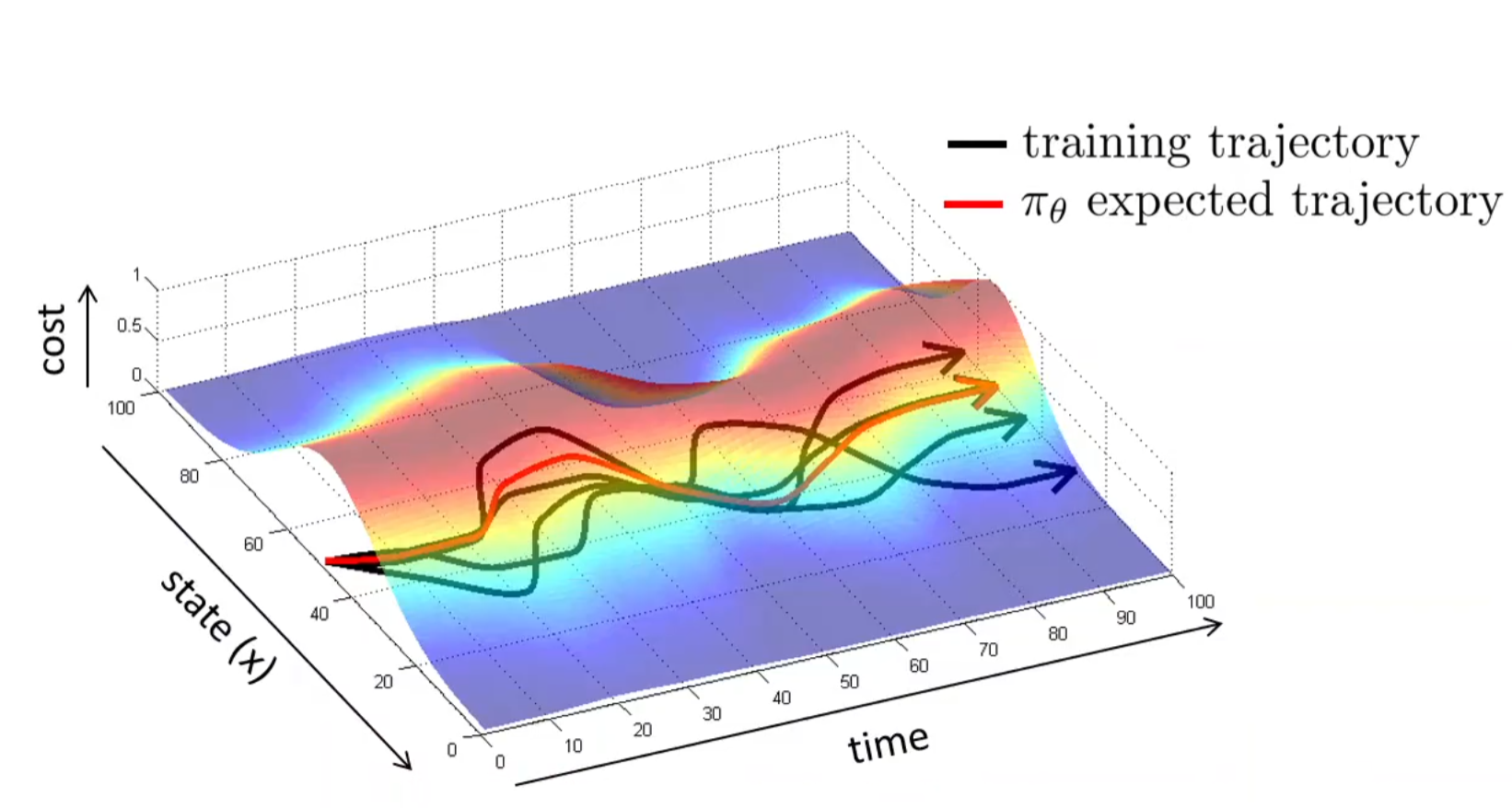
Be smart about how we collect (and augment) our data
正如上一节中的insight所提到的,制作训练集的时候可以人工的制作一些错误,并且对应地修正。这样policy model在inference的时候,即使犯了一个错误,进入到了下一个不正确的observation中,但是由于训练集中有对应的correction训练,model将懂得如何进行修正。示意图如下:在多条训练轨迹下,observation分布将会扩大,而其扩大是通过(人为)犯错并纠正而扩充出来的。
另一种技巧是'fake' data,比如说在驾驶训练中,不止有前面的正方摄像头,同时也有左前方和右前方的摄像头,模拟‘不小心’方向盘左打/右打的场景,并且方向盘当前方向与摄像头的相对方向就是correction。
Use powerful models that make very few mistakes
假如说模型犯错的概率\(\epsilon\)非常的小,那么其实也是能够接受的。因此可以考虑如何让这个概率非常的小。为什么实际中之前介绍的训练范式通常不work?
一方面是人类行动的非马尔科夫性质:之前所介绍的policy全都是基于当前的observation来给出action,但是很明显人类不是。我们会往往会刻意或潜意识中考虑过去历史的一系列操作,但是我们之前的建模中没有这个inductive bias。因此一种解决方式便是考虑一种加入了这种归纳偏置的模型,如下图:
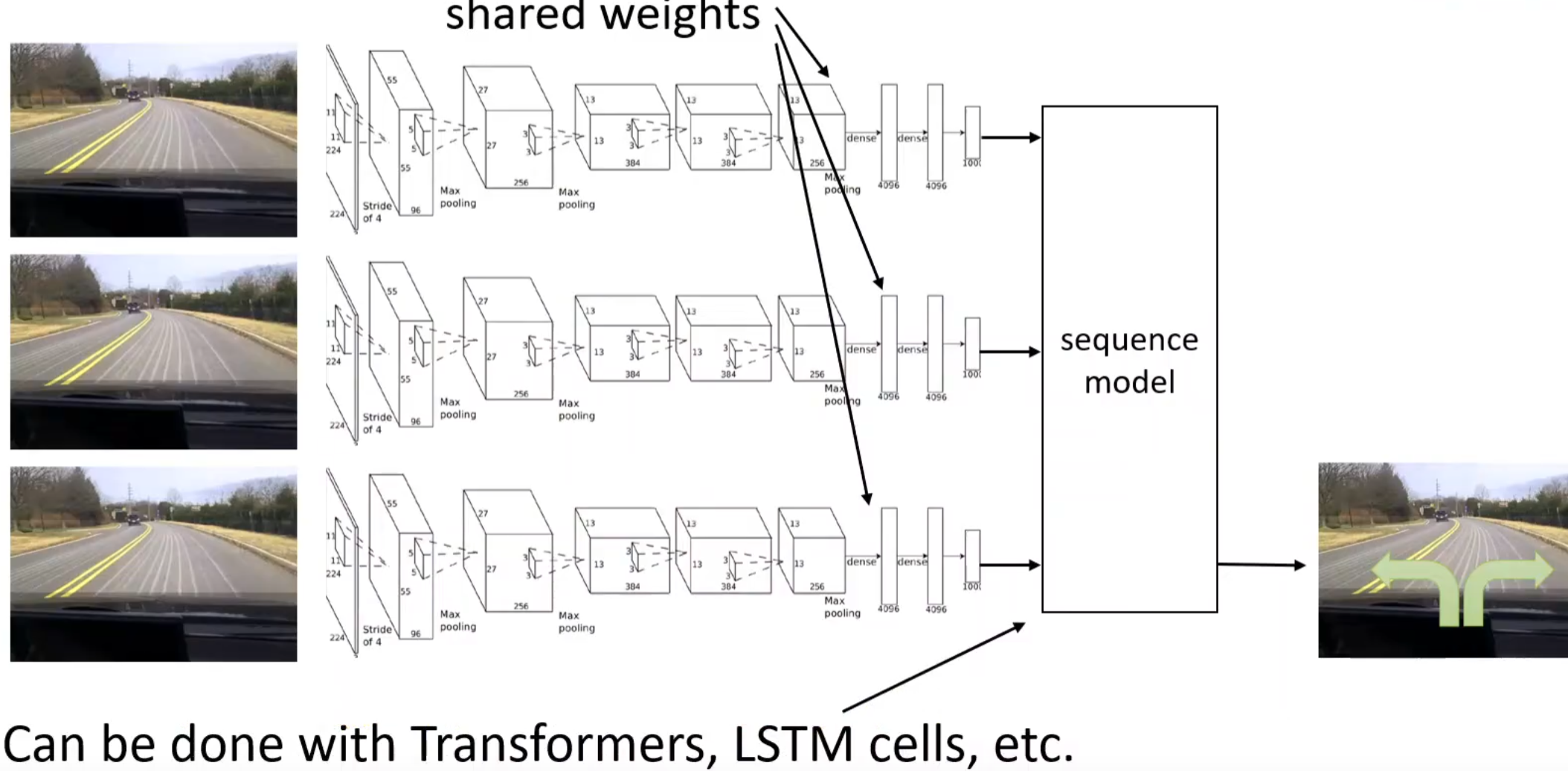
但是,这样做不一定能够提升表现,原因出在因果混淆(causation confusion)。这听起来很反直觉,举一个例子:假如说一个车,踩下刹车的时候灯将会亮起。在人出现在前面的时候,踩下刹车,然后灯亮起。但是模型学习过去很多切片的时候,就可能认为:踩下刹车的决策可能是因为灯是亮着的原因,但其实是人。

另一方面是multimodel behavior。假如说在面临一个场景的时候,多个选择是可以被接受的,这在离散的action空间中是可以用概率来表示的,但是在连续空间的action表示中,用一个简单的分布来建模多种action是十分困难的。比如说只用一个高斯建模action,那么左和右的两种action的''平均''将会非常糟糕。
解决这个问题,第一种方式是使用更有表达能力的分布。常见的有:
- Mixture of Gaussians
- Laten variable models:输入的不只有原来的input,还有一个基于先验的随机的分布中选取的随机参数。这一种最常见的是(conditional) variational autoencoder,之后将会介绍
- Diffusion models
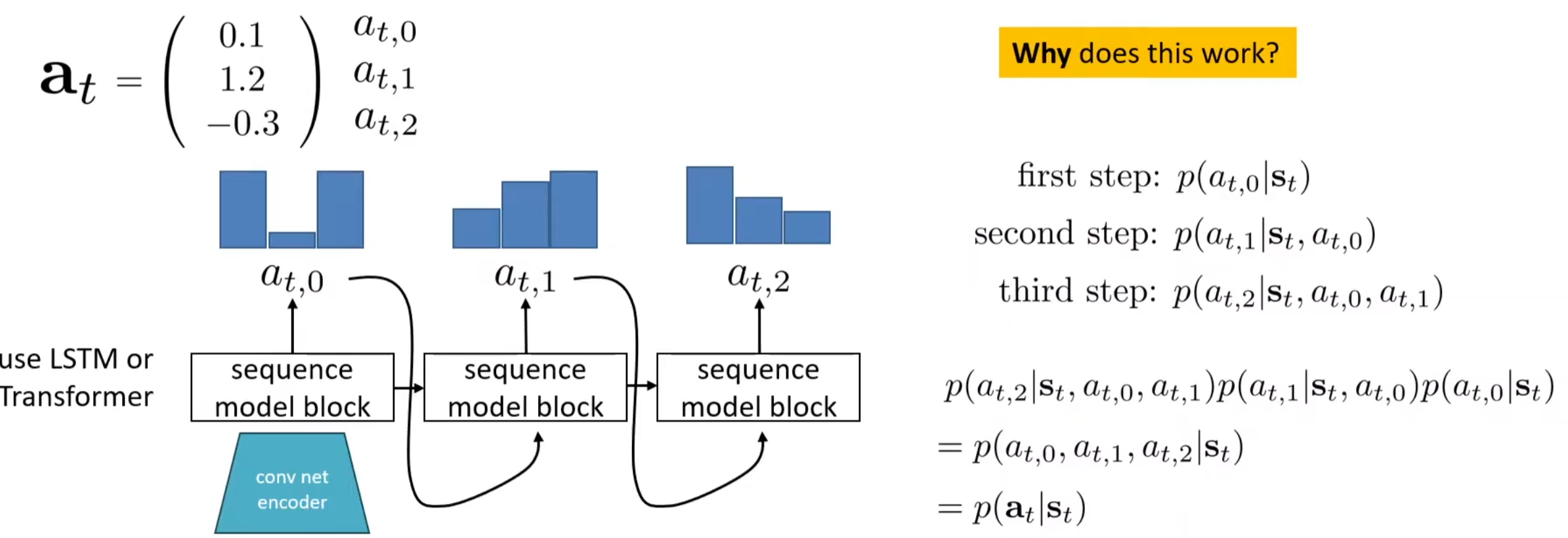
第二种方式是离散化。比如说在无人机飞行中,规定动作只有向前、向左、向右。但是其实这种在实践中很难应用,尤其是在高维空间中很难引用。因此,常见的是对于维度进行离散化。注意:将一个维度进行离散化是能够接受的!一种常见的按照维度来进行离散化的方式为autoregressive discretization:
Use multi-task learning
听起来很反直觉:其实让模型学习多项任务实际上可以使模仿学习变的更加简单。如果说原来的任务就是到达地点,然后制作数据集的时候还需要专家认为的制造错误并修正,这很不方便;但是如果考虑到达多个目的地,然后训练的时候也不说到达的是哪个目的地,那么这样就可以拓宽状态空间了。
也称为goal-conditioned behavioral cloning
虽然理论上很好,但是实际上有两处distribution shift:一种是之前所说的\(p_{data}(o_t)\neq p_{\pi \theta}(o_t)\),另一种是\(goal_{train} \neq goal_{\pi_{\theta}}\)
Change the algorithm (DAgger)
之前在模型上的trick都是尽可能的让epsilon小,以尽可能地\(p_{data}(o_t)=p_{\pi \theta}(o_t)\);但是能不能反过来,在制作数据集的时候就实现这一点呢?这其实就是第一种approach:Be smart about how we collect (and augment) our data的思路。那么DAgger,Dataset Aggregation,在训练一轮之后,进行inference,不论结果的正确与否,对于inference的observation都打上action label,把这些数据加入原来的数据集,然后再训练。不断循环,直到策略收敛。

其中较为麻烦的可能是第三步。比如说驾驶场景,让人类offline地对场景做出决策判断可能不是很自然,人们更自然的是online决策,即开车的时候做出自然的决策。后续有很多的工作就是克服这一‘不自然’。