Markov Decision Process
在课程最开始的状态搜索树或图中,一个显著的过程特征就是:所有的过程都是确定性结果,agent采取了这个操作将会面临什么样的对应的结果。但是如果是不确定性搜索呢(Non-Deterministic Search)?即:采取了一个行动之后,对应的并不是唯一的确定性状态,而是有着概率分布下的状态可能结果。
Award
在强化学习中,award是一个非常重要的用于改进policy的措施;这里也是如此!考虑如下的一个小例子:
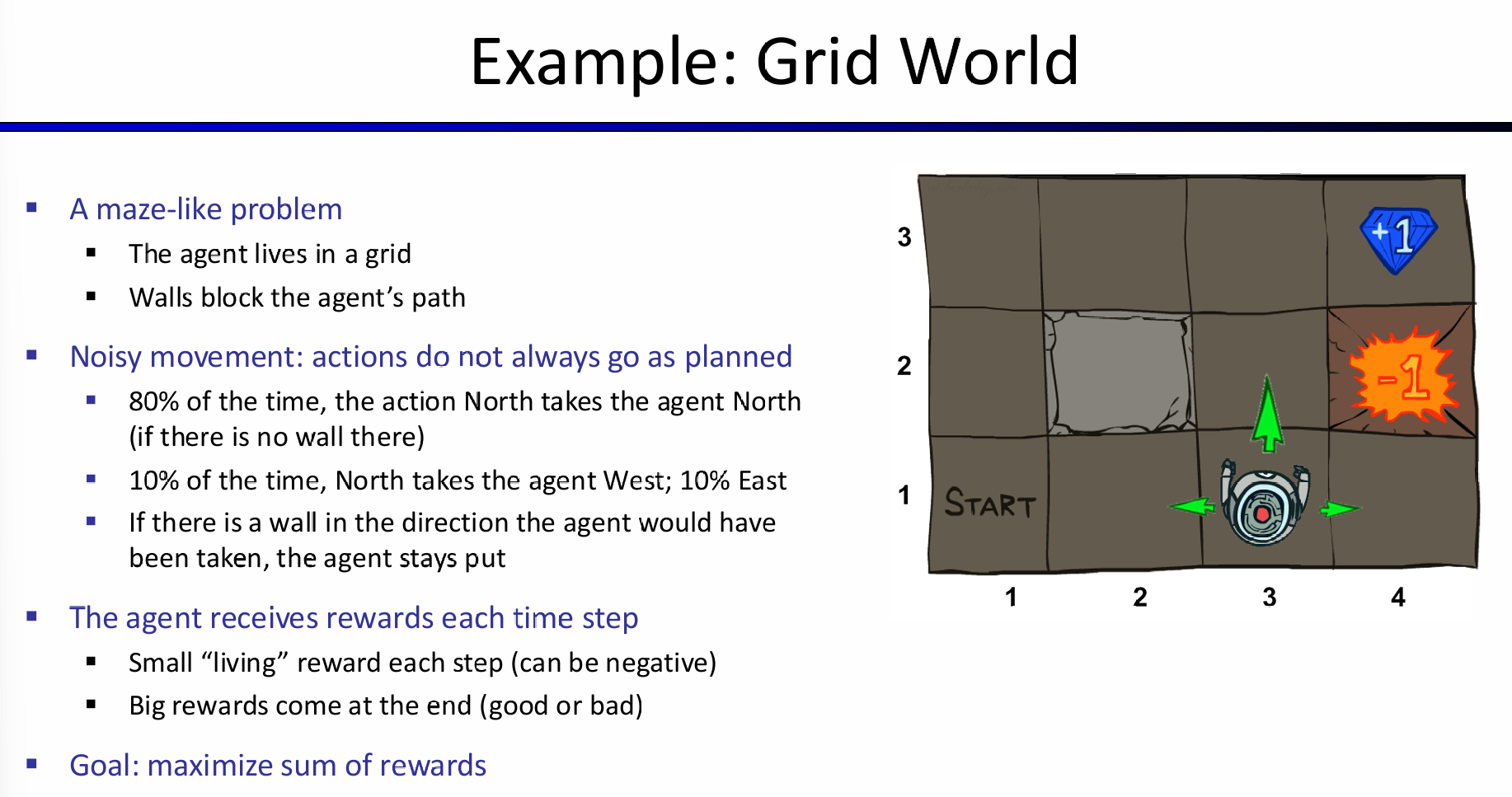
假设现在采取的行动只有一种:那就是移动一格;而这个行动的结果的可能情况如图所示。那么如何设计award呢?首先明显地,可以认为抵达钻石就是+1,并且游戏结束,而火坑就是-1,并且游戏结束;而其次,我们希望小人能够尽可能的活下来,那么就可以设置一个非常小的负数award(如果是整数,那么岂不是一个安全的地方不断撞墙,award就能无限大)。agent可以根据这个award来更改Action Policy。
那么神奇的地方就来了:如果我希望机器人能够尽可能快一点找到钻石,那么可以设置这个负数的绝对值稍微大一点;但是设想一下,如果过大,那么机器人极端一点可能先考虑会找火坑跳入!因为award负数太痛苦了,机器人只想快点结束游戏,钻石,甚至是直接进入火坑寻死,那么都在agent视角看来,是合理的policy。
Markov Decision Processes
Concept

在这里,马尔科夫的含义其实是;下一步的结果仅仅与当前的状态和采取的行动有关,与过往的任何东西都无关。这一点其实和deterministic搜索问题中的successor function较为类似,都和历史无关,只与当前state有关。
Policy:In deterministic single-agent search problems, we wanted an optimal plan, or sequence of actions, from start to a goal。而在MDP中:

注意这里的policy不是规划好了未来直到最终状态的所有计划步骤,而是单独对每一个可能的状态s都分配一个最优的行动。
Example: Racing
在上面的例子中,action对应state的概率分布这一点,其实在情景设定中体现的并不明显。现在见下例:
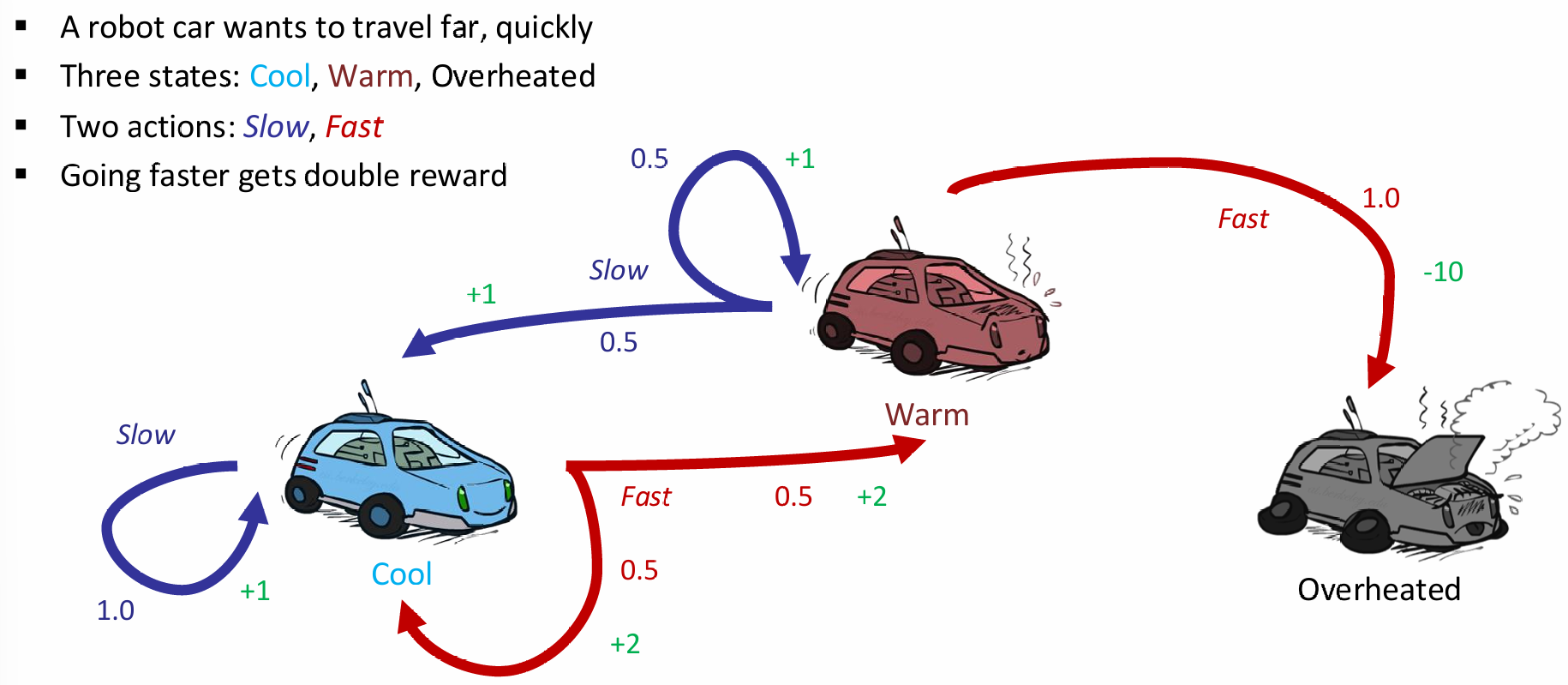
车子有三种状态:cool warm and overheat,在前两个状态可以选择加速或减速,而在overheat就gg;最大的特点就是选择了action,对应的下一个状态并不是确定的,而是有概率分布的。
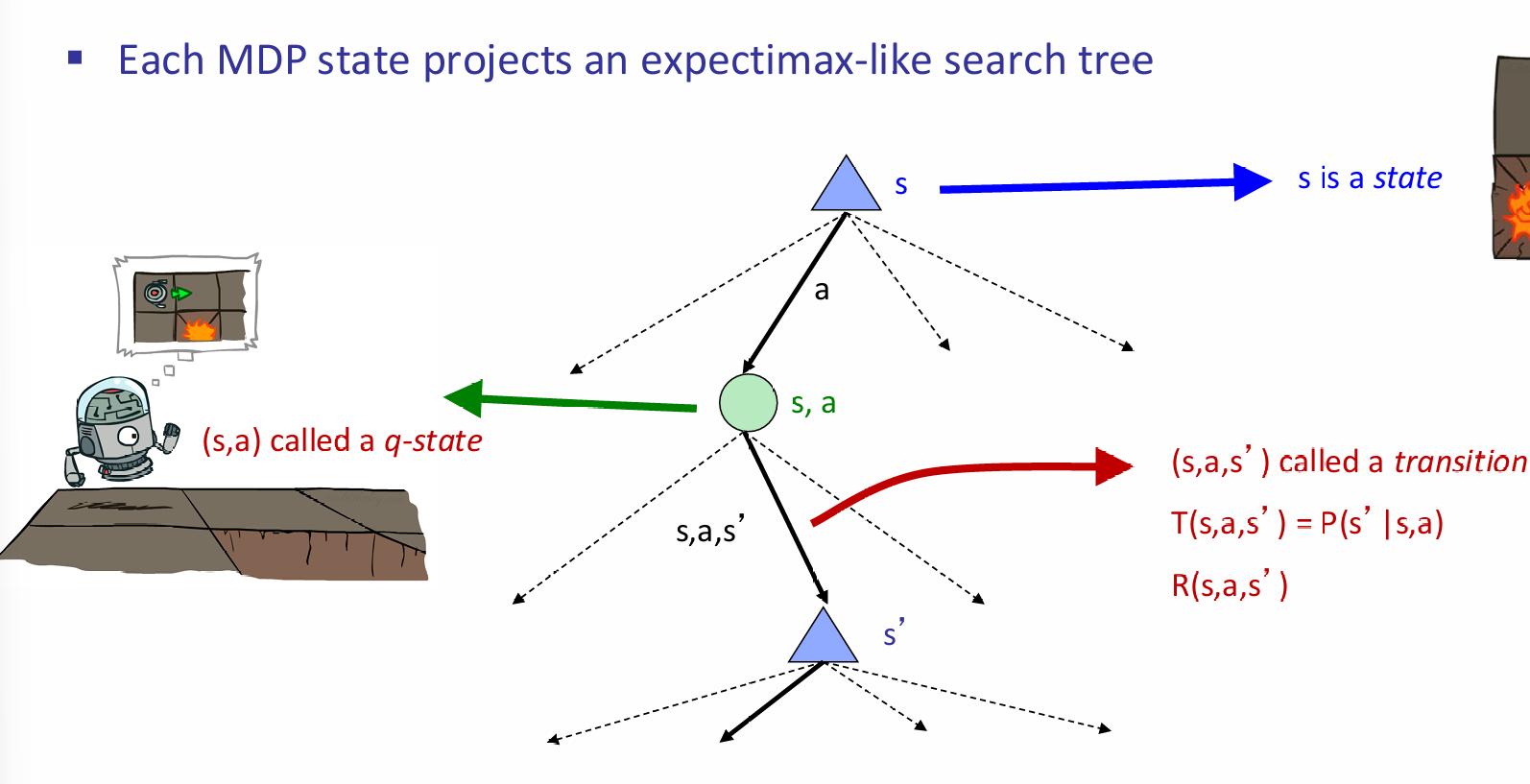
如何用一个搜索树表达这种可能性的概念呢?甚至,比如说,在cool状态,两种action都可能导致下一个状态还是cool。这究竟如何表示?这里,引入了(s, a)q-state节点,来表示当前状态s所采取的状态a,然后下面紧跟着的是所有可能的下一状态及其概率:
那么应该agent如何选择action preferences呢?假如说两条路,都是四步,一条是一步+1分,而第二条是最终一步+4分,虽然award都是一样的,但是很明显第一条是更合理的。总结:

对于一个当前窗台来说,我们可能会考虑后面很多步的,但是鉴于刚才的说法,我们更倾向于更早,甚至是现在,的高回报,所以对之后的q-state节点所代表的utility(award)值会乘上一个衰减系数。
Solving MDP
 9
9
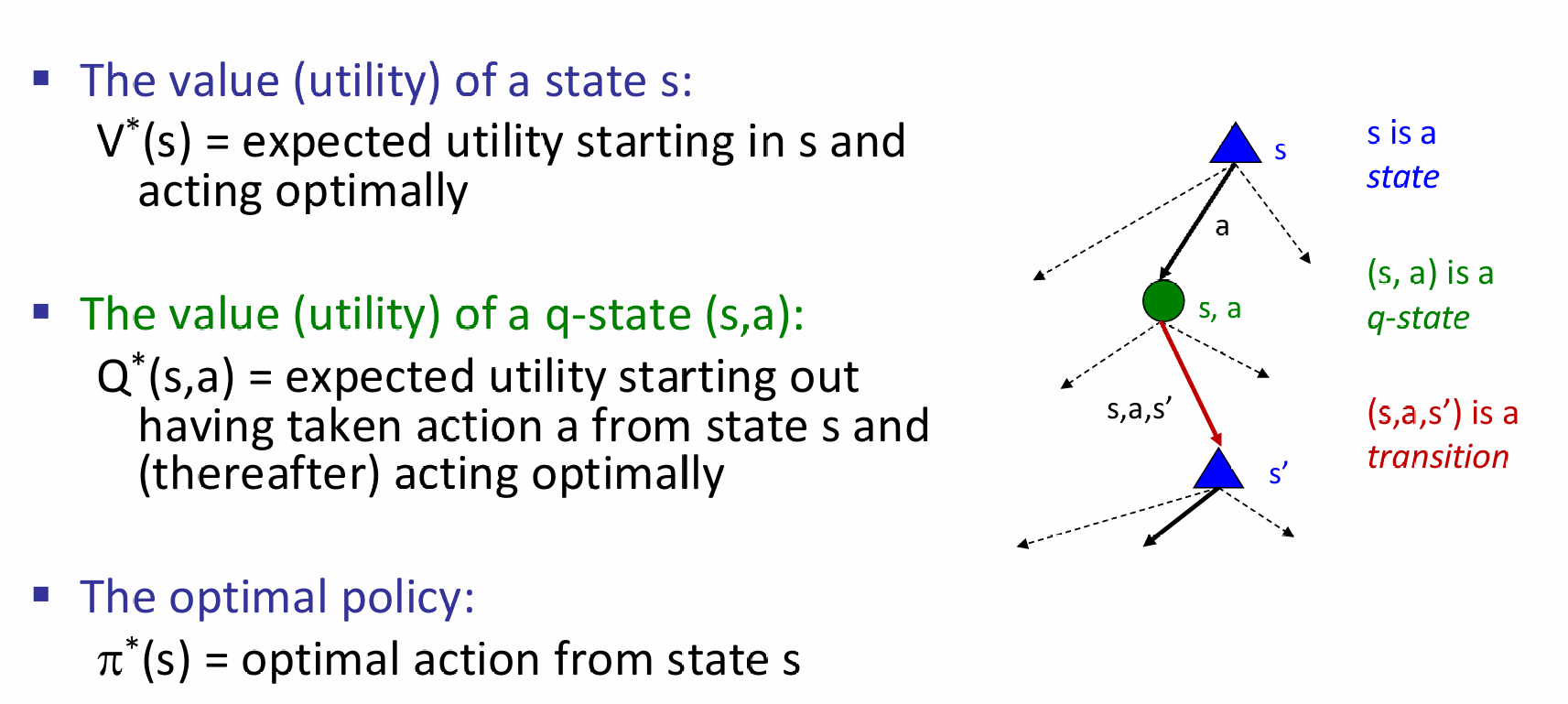
每一个state节点都要选择期望utility最大的q-state node,i.e.,其所代表的a action。而q-state utility又是如何计算的呢?又是需要其所连接的所有的state的utility值,而这又是怎么来的?又要看q-state node。可见这是一种recursion:

对于这样的一个问题,如果采用了expectimax的方法,那么有两个问题:第一是大量的表示同一state的node将会被重复创建,space complexity不友好;第二是这个树深度可能会很高,那么计算复杂度就上来了,但是又注意到由于衰减系数的存在,树深层部分切实作用并没有想象中的大。
因此,我们可以采用bellman equation的经典问题:动态规划!这种方法称为:value iteration
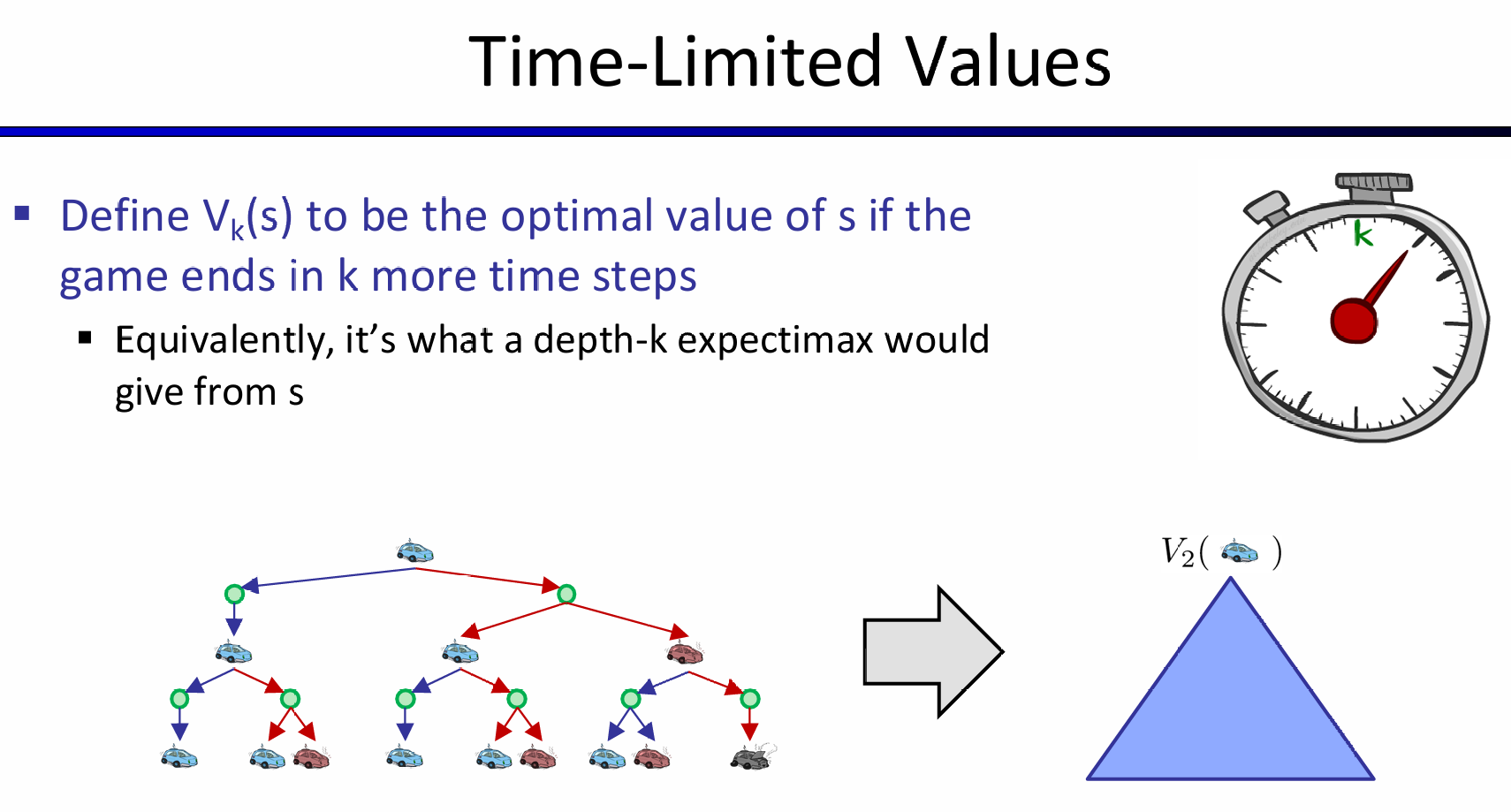
这里创建的\(V_k(s)\)与Time-Limited Values就是对应规划问题中的'step'概念。那么推的时候,可以从k=0开始推,而这时候认为utility都是0(注意utility of node 以及 award represented by \(R(s,a,s')\)是不一样的).

这里的Theorem其实说明的是:动态规划最终会向不动点收敛
以小车racing例子为例,展示推Vk(s)的过程中的两步,并且假设衰减系数是1:
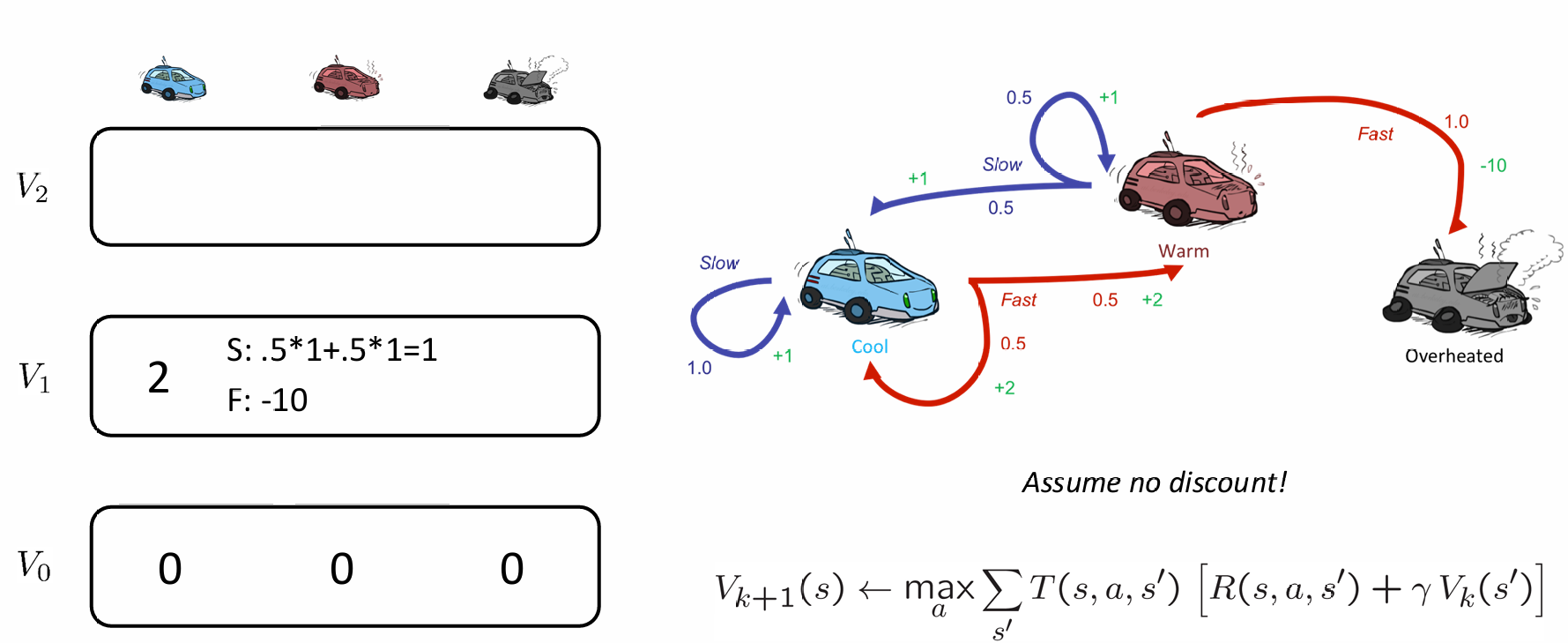
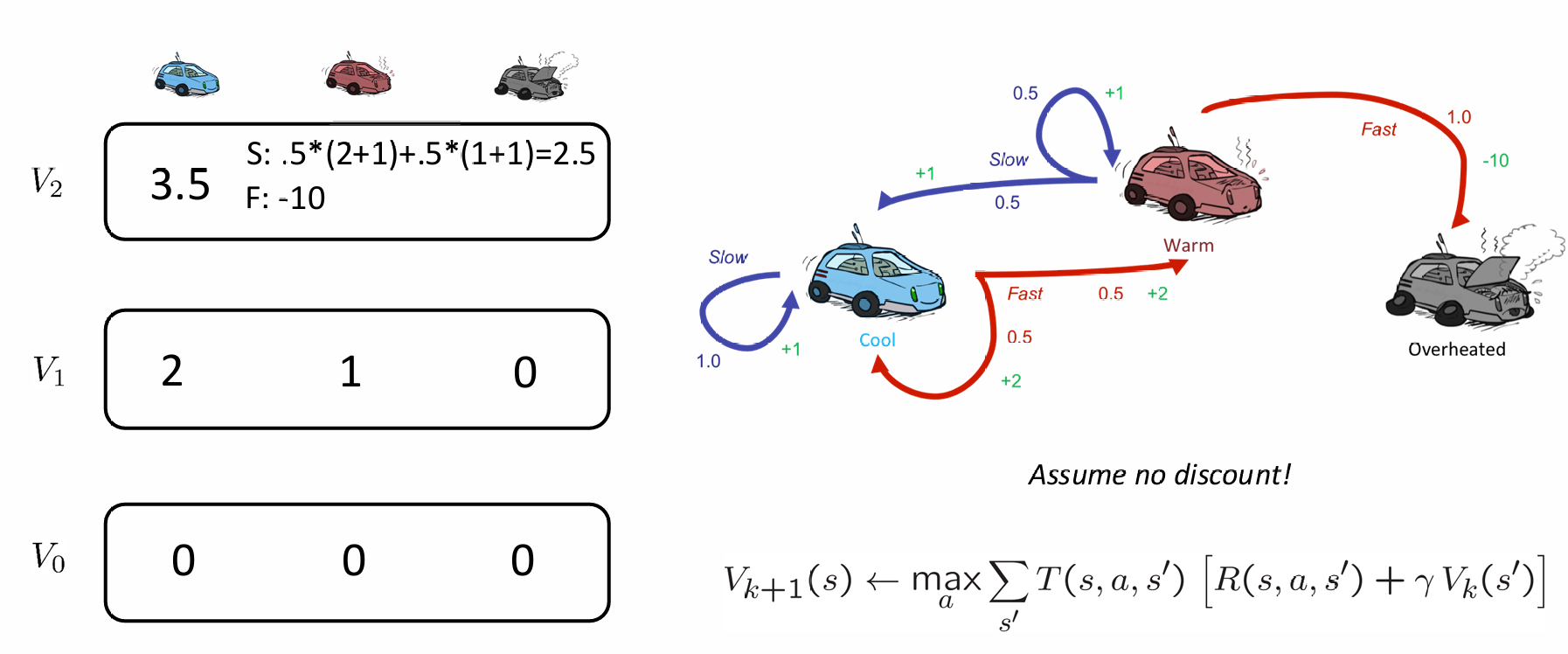
在经过了大量的iteration之后(k非常大),最后这些状态的utility值将会稳定,代表该状态真实的optimal utility值。
原来在search problem中,在获得了所有state的utility之后,要经过policy extraction,才能获得optimal solution了:

但是如果有了optimal utility with action probability,i.e.,Q-values,那么action将会十分的明显:
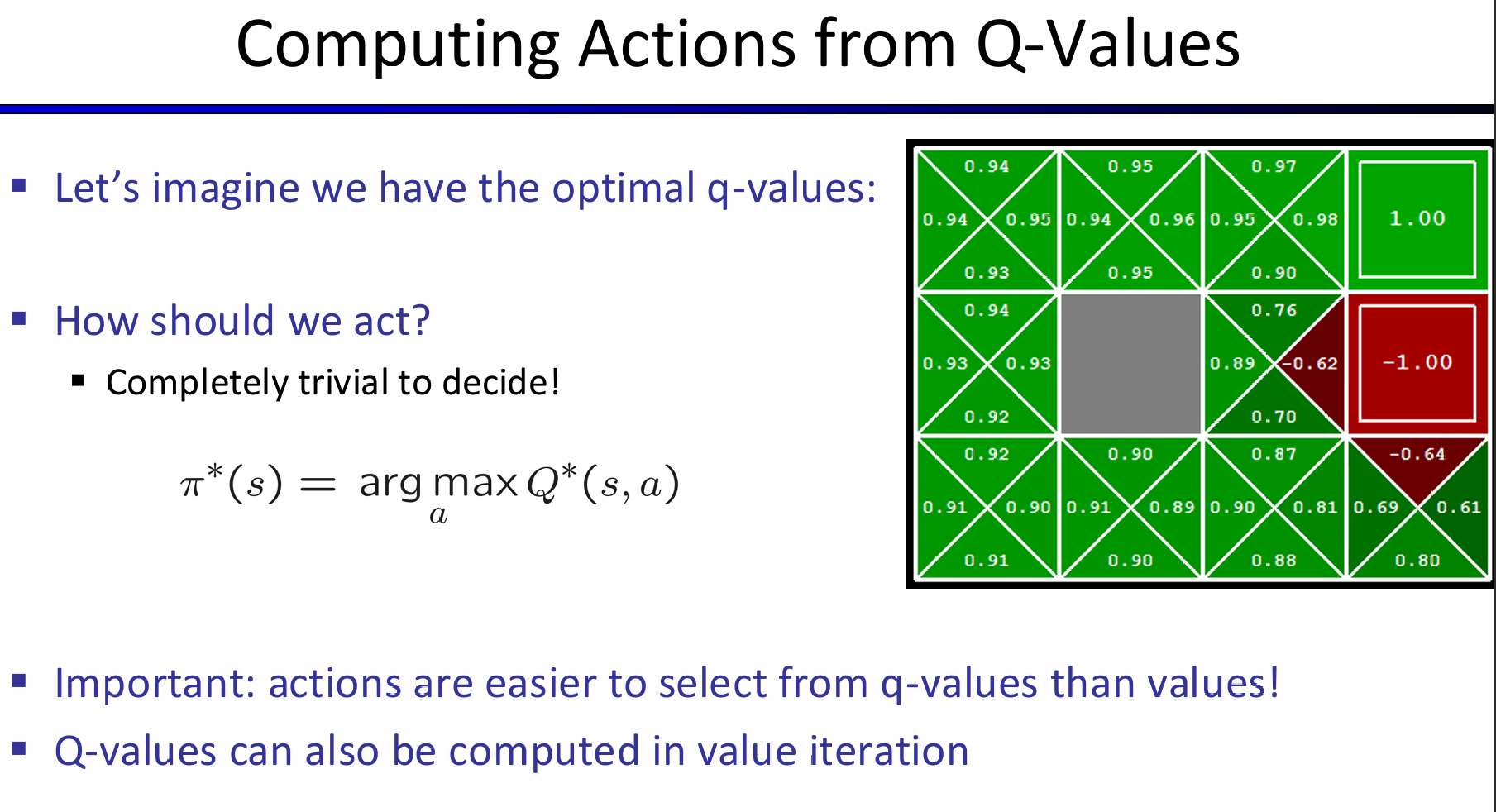 因此有一种算法变体,就是Q-value Iteration:
因此有一种算法变体,就是Q-value Iteration:

Policy Iteration
上述方法好是好,但是复杂度很高:\(O(S^2A)\)一次循环。而且事实上:policy经常在值很早之前就收敛了。根据上述两个客观事实,我们可以考虑policy iteration:
step1: Policy Evaluation:calculate utilities for some fixed (not optimal) policy
step2: Policy improvement: update policy using one-step look-ahead with resulting converged (but not optimal!) utilities as future values
Repeat steps until policy converges
这最终得到的policy最终仍然是最优的。并且在某些情况下能够收敛的非常快!在fixed policy中,do what \(\pi\) says to do, not the optimal action. 对于一个fixed policy,utility的计算还是十分直观的:


直到如何计算utility之后,如何根据它来改进Policy呢?
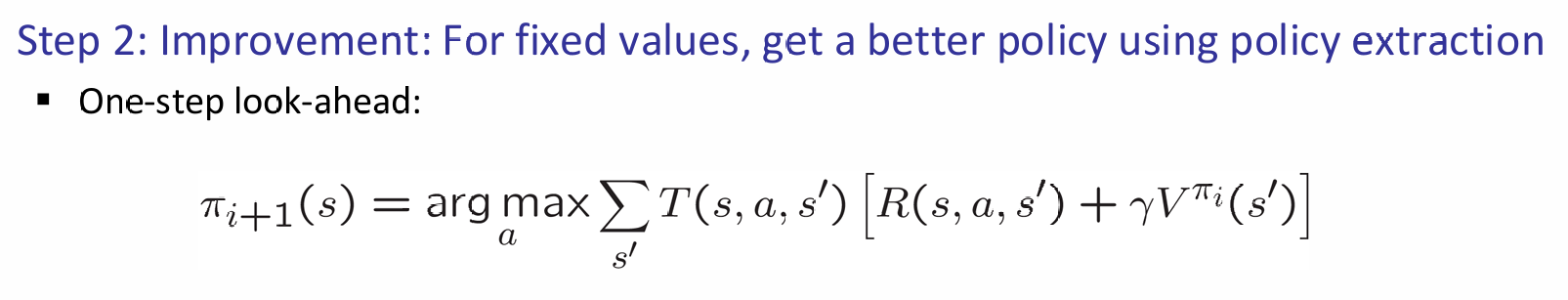
Summary
