矩阵计算与自动求导
矩阵计算——矩阵怎么求导?
函数知道如何求导,而且还知道链式法则。但是深度学习中都是矩阵操作,而且同样需要使用梯度进行参数优化。那么如何对参数求导呢?即:如何将导数拓展到向量?
原来都是\(\frac{\partial y}{\partial x}\),但是现在x y这两个参数中的任意一个都可以是变成向量: 第一种:\(\frac{\partial y}{\partial \vec x}\)。如果x向量是列向量,那么得到的结果会是横向量。下面图片是一个例子(\(y=x_1^2+2x_2^2\)):
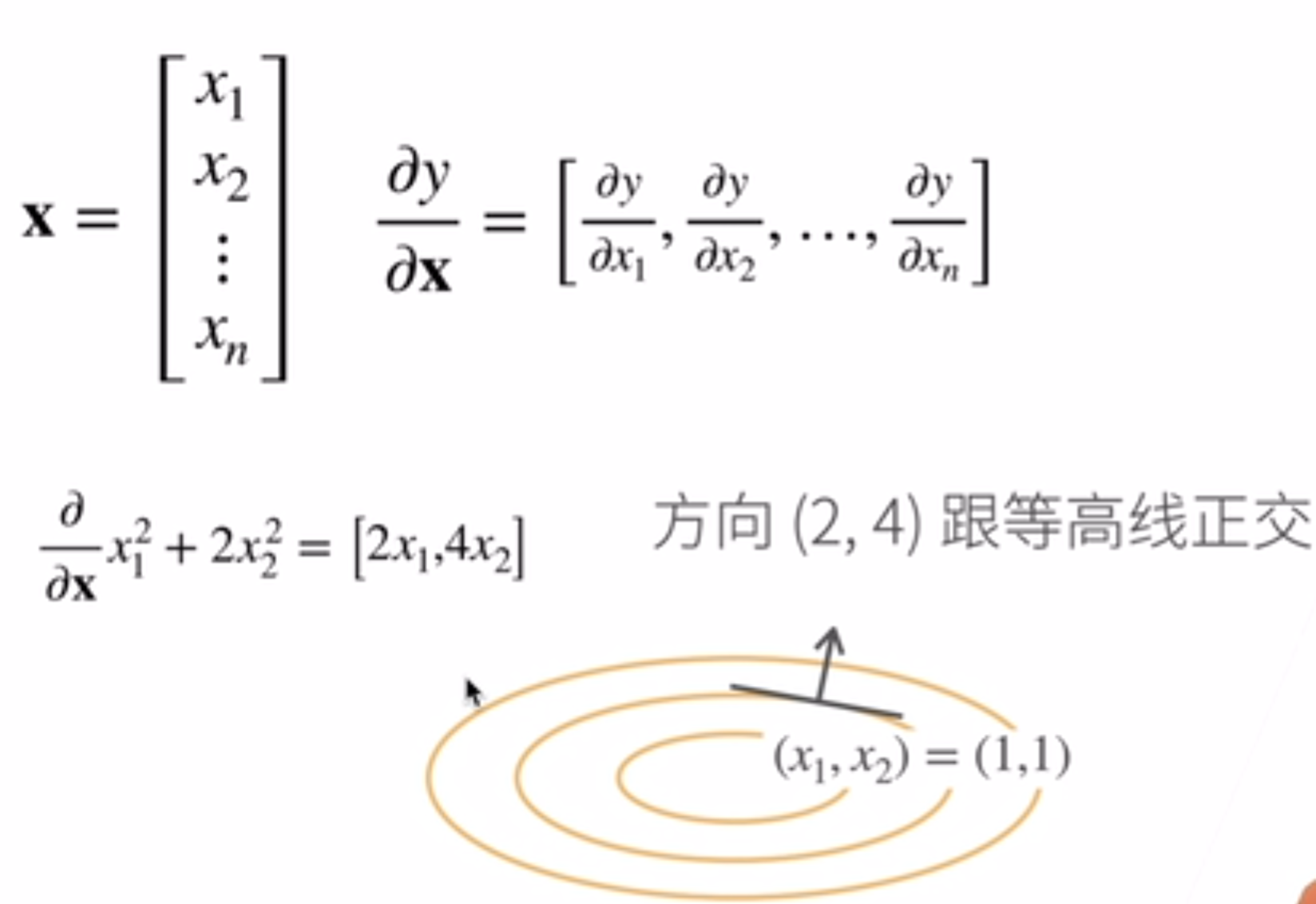
这种情况还较好理解,主要是列向量变为行向量的变化一开始可能不好理解。我是这么理解的:这个函数y可以泰勒展开,那么就会有导数×(自变量-初始值)这一项,那么这个乘法中后者是列向量,那么前者是行向量的话就能成功得到标量的结果;当然,这种理解是个人且粗糙的。同样,这种类型的导数有一些经典的公式如下:

第二种:\(\frac{\partial \vec y}{\partial x}\)。这中就比较好理解了,因为可以把y向量中的每一个值都是为一个x相关的函数,因此很容易认同的得到的结果是列向量(如果y是列向量的话)。示意图如下:
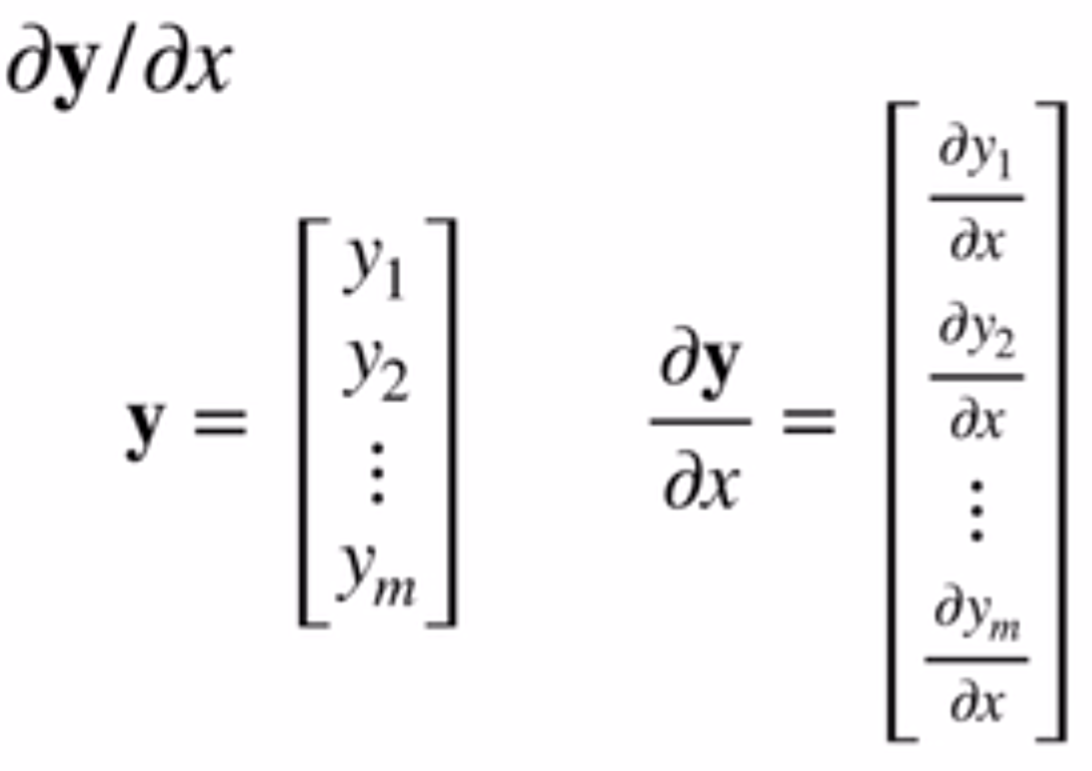
最后是\(\frac{\partial \vec y}{\partial \vec x}\)。在前面两种的介绍之后,就更容易理解和认同了。y向量中的每一个元素都和x向量有关,因此每一个元素得到的导数是一个行向量,那么整个y向量的导数就是一个方形矩阵了。示意图如下:
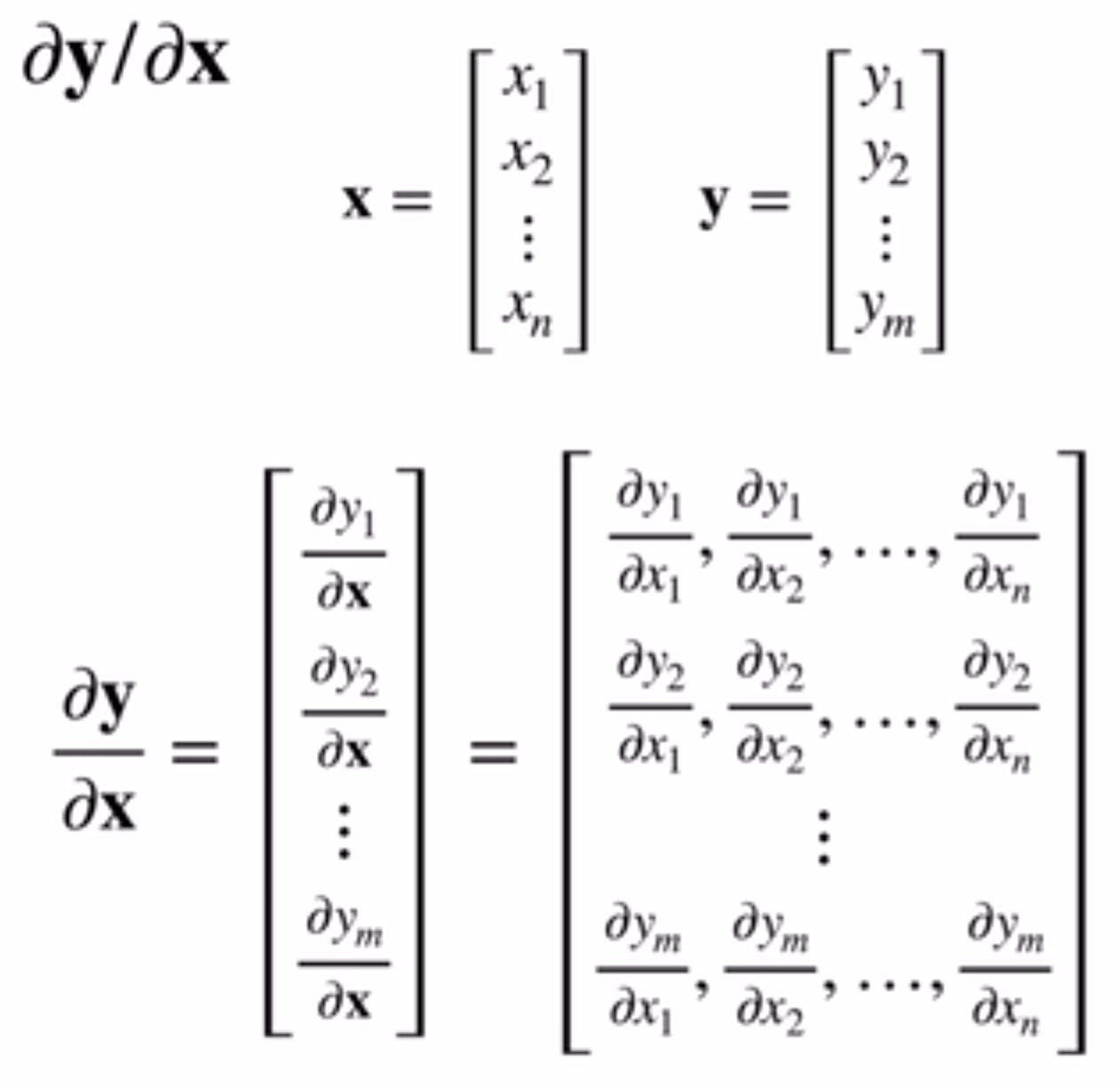
一下是一些这类导数的样例:

自动求导
x y都是标量的情况中的链式法则已经很熟悉了,那么向量中依然有这种链式法则,但是关键在于要把形状理清楚。矩阵求导的链式法则的几个例子如下:
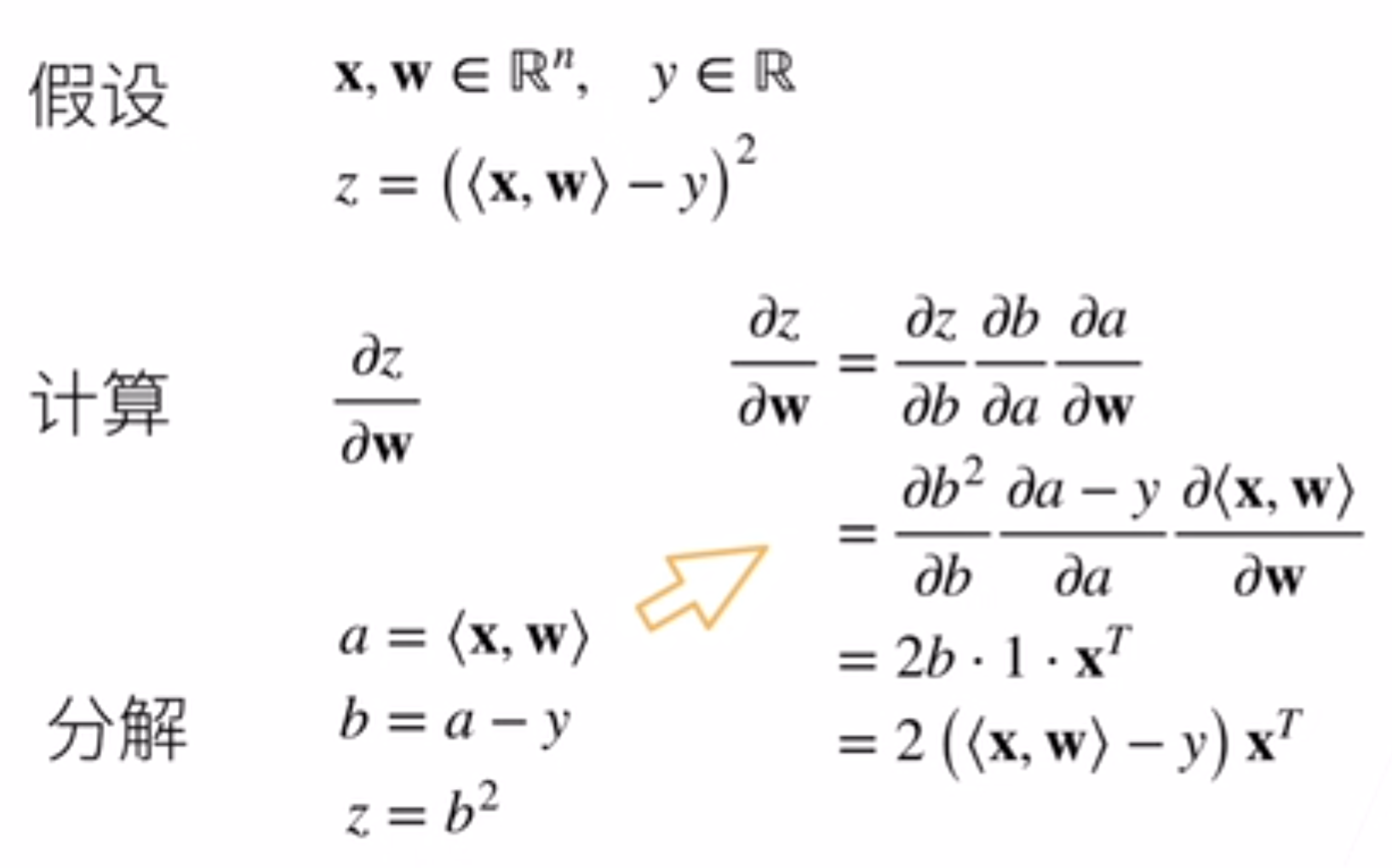
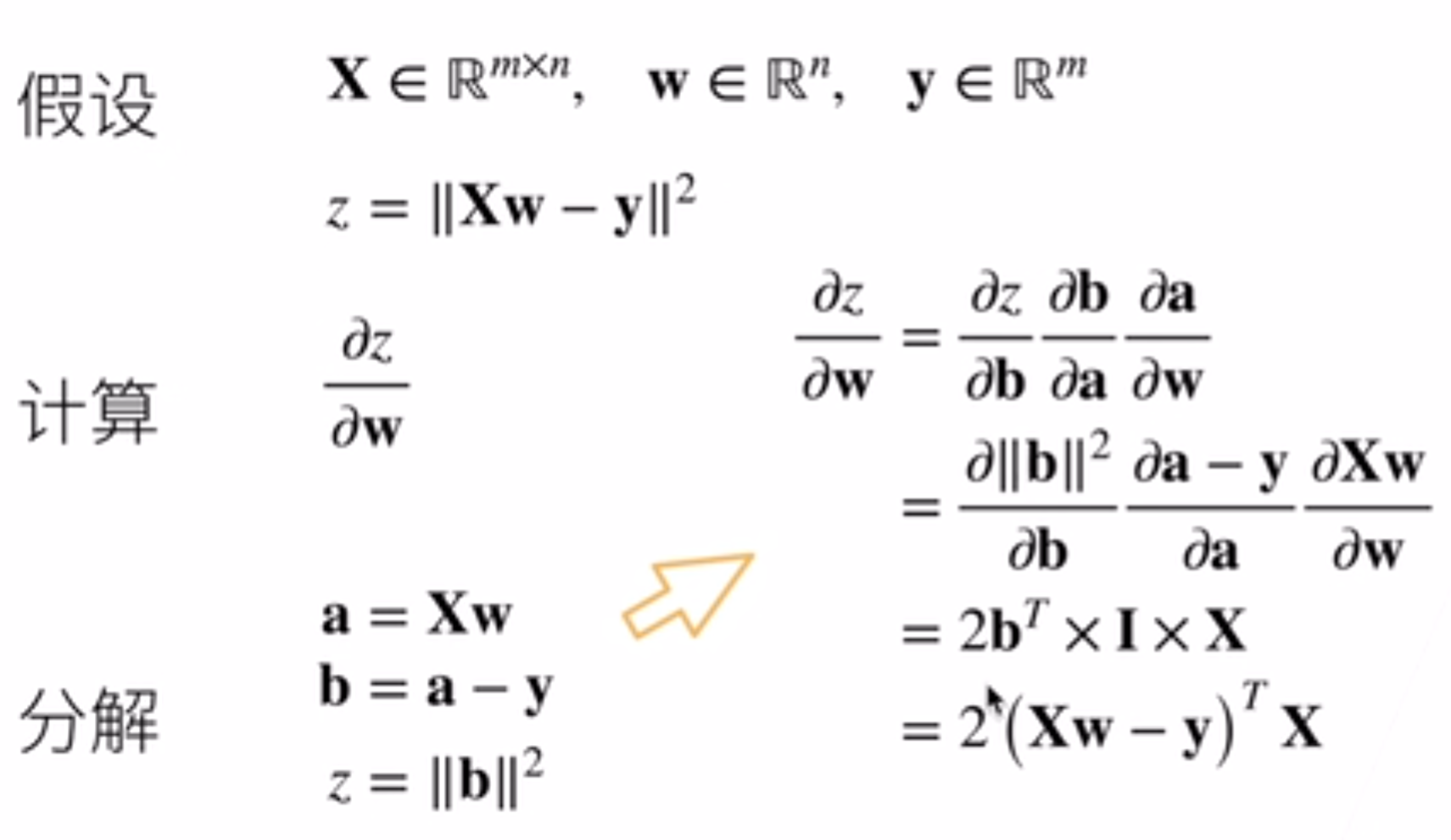
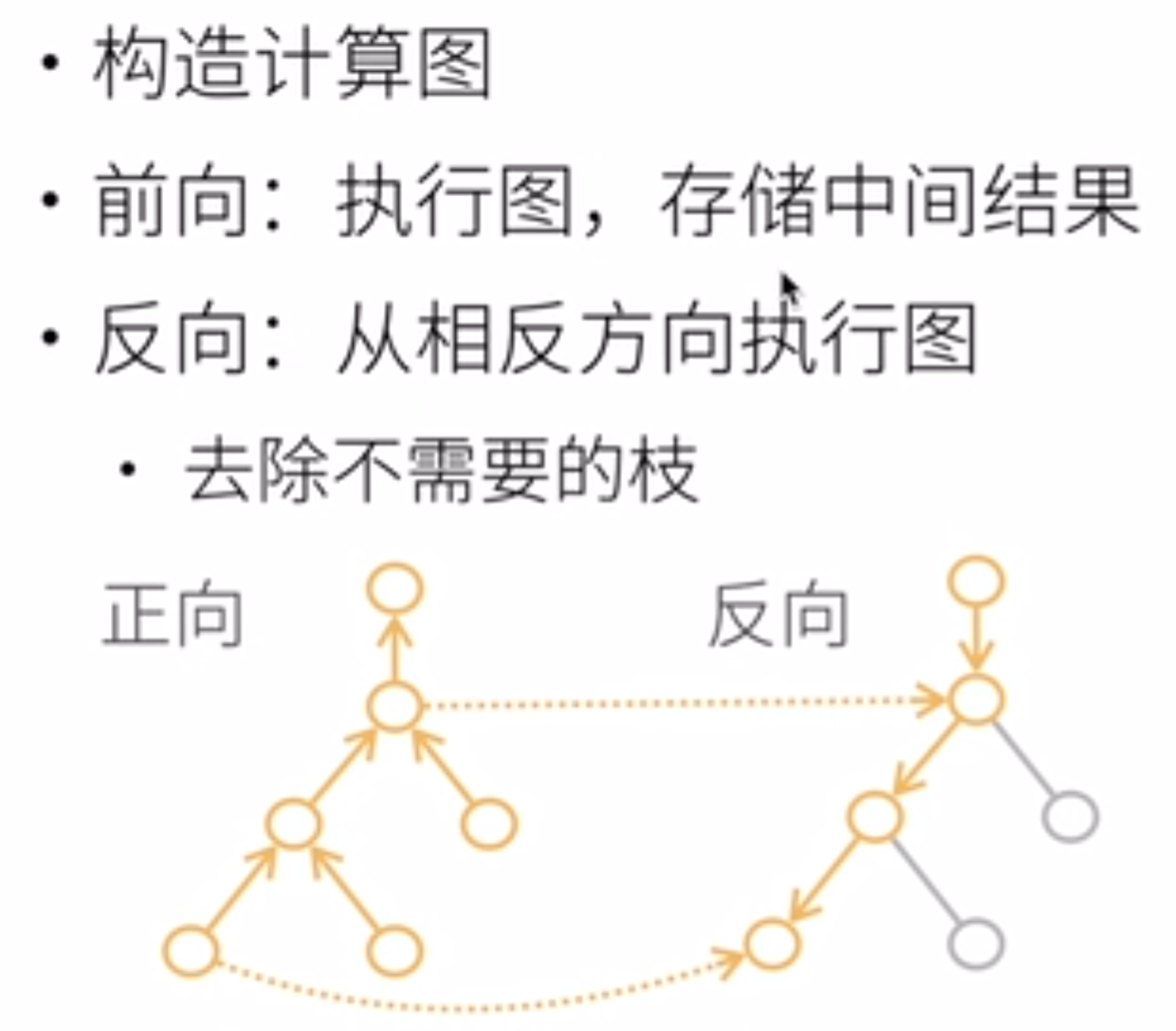
大致了解了矩阵的链式法则之后,pytorch中是如何实现自动求导的呢?pytorch会把代码分解成操作子,并且把计算过程表示成一个无环图,那么链式法则对目标求导的时候就能按图索骥了。链式法则可以分为正向和反向,如下图所示:

在反向拿到表达式之后,仍需要代入值进入,这个值哪里来呢?那么就是一开始在构建完图之后就可以执行一遍图,把中间参数的结果都算出来并保存,然后反向计算导数的表达式,把之前正向执行得到的结果代入。那么在反向传播的过程中,一个很大的GPU内存开销就是用来储存这些中间结果,因为如果n是操作子个数,那么计算复杂度就是O(n)。
那么pytorch中是如何通过代码进行自动求导的呢?值得注意的是:Pytorch中操作无环图的构造是隐式的。实例代码如下:(假设我们想对函数\(y=2\mathbf{x}^{\top}\mathbf{x}\)关于列向量\(\mathbf{x}\)求导)
import torch
x = torch.arange(4.0)
x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True)
# require了grad之后,就可以通过 x.grad来访问它的梯度值了
y = 2 * torch.dot(x, x)
y.backward()
x.grad
# 为什么是x这里获取梯度值呢?因为x归根到底是自变量,而且深度学习中更新的参数是x
# tensor([ 0., 4., 8., 12.])
x.grad == 4 * x
# tensor([True, True, True, True])
# 现在计算另一个函数
# 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值
x.grad.zero_()
y = x.sum()
y.backward()
x.grad # tensor([1., 1., 1., 1.])
在默认情况下,PyTorch会累积梯度,我们需要清除之前的值
同样,pytorch可以手动控制哪些参加链式法则:这里可以分离y来返回一个新变量u,该变量与y具有相同的值,但丢弃计算图中如何计算y的任何信息。换句话说,梯度不会向后流经u到x。因此,下面的反向传播函数计算z=u*x关于x的偏导数,同时将u作为常数处理,而不是z=x*x*x关于x的偏导数。
x.grad.zero_()
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
x.grad == u # tensor([True, True, True, True])
使用自动微分的一个好处是:即使构建函数的计算图需要通过Python控制流(例如,条件、循环或任意函数调用),我们仍然可以计算得到的变量的梯度。