3DGS
3D Gaussian Splatting for Real-Time Radiance Field Rendering
Motivation
However, achieving high visual quality still requires neural networks that are costly to train and render, while recent faster methods inevitably trade off speed for quality.
辐射场发展迅速,但是神经网络总是面临着quality(拟合程度)与时间的trade-off,而时间与fps又息息相关。于是能不能快速地进行3D环境重建呢?这篇工作的目标便是如此:
We introduce three key elements that allow us to achieve state-of-the-art visual quality while maintaining competitive training times and importantly allow high-quality real-time (≥ 30 fps) novel-view synthesis at 1080p resolution.
三个key elements分别是什么呢?
- Represent the scene with 3D Gaussians that preserve desirable properties of continuous volumetric radiance fields for scene optimization.
- Interleaved optimization/density control of the 3D Gaussians, notably optimizing anisotropic covariance to achieve an accurate representation of the scene.
- Develop a fast visibility-aware rendering algorithm that supports anisotropic splatting and both accelerates training and allows real-time rendering.
3D Gaussian Ellipsoid
在CG geometry中提到过Constructive Solid Geometry(CSG),尝试用基本几何形体之间的Boolean operations去合成复杂的几何体,但是如果基本几何形体太多,肯定不方便网络和优化。那么有没有一种高度参数化的、方便优化的基本几何形体呢?论文中创新性地使用了3D Gaussian Ellipsoid来作为基本几何形体。中心点定为μ (x, y, z),然后通过一个协方差矩阵(covariance matrix)去定义椭球的大小和形状。高斯用真实世界坐标系下的协方差矩阵∑来进行定义:
但是在渲染成2D的时候,要以摄像机为原点的笛卡尔坐标系,因此需要对协方差矩阵进行变换,从而得到摄像机视角下的、将进行光栅化的3D高斯椭球:(变换有两点:一个是frustum->cuboid,i.e.,projective transformation;另一个是translation,即viewing transformation)
至于为什么公式长成这样,这是因为涉及到保持协方差矩阵的半正定性质。这在协方差矩阵变换的上下文中非常重要,确保变换后的矩阵依然是一个合法的协方差矩阵。那么正定矩阵长什么样子呢?假设有一个单位球,然后我在三个坐标轴方向放缩,然后进行旋转,那么一个大致的椭球就出来了,虽然不是高斯分布。因此:Given a scaling matrix 𝑆 and rotation matrix 𝑅, we can find the corresponding Σ:
注意到这个矩阵也是半正定的。R S矩阵定义了方向,和椭球的三个轴向的长度,然后配合第一个G(x)公式对表面进行高斯分布。论文中用一个三维向量s来表示放缩(xyz轴放缩系数)和一个四元数q来表示旋转。因此,对于高斯椭球来说,这个是explicit representation,但是用高斯椭球表示geometry又是implicit representation。在上述的定义之后,基本几何体——高斯椭球终于定义完毕,高度的参数化使得它容易被优化(optimized),且表面的explicit representation公式可微,使得它可以进行梯度下降。
Spherical Harmonic for Color
一个高斯椭球应该有哪些property?除了3D Position,协方差矩阵,还应该有什么?首先想到应该是类似于NeRF中的density,而论文中,不透明度用opacity α表示。通常情况下,对于一个基本单位的高斯椭球,只有一个opacity值。那么还有颜色呢?这就有些麻烦了,因为椭球上有很多的点,不像NeRF那样用光线方向向量就能知道一个点的RGB值(5D函数)。那么如何给椭球上的点来一个"5D Function"呢?论文中就使用了球谐函数的方法拟合颜色。
球谐函数可以把复杂的颜色变化用一些数学函数来表示,就是把颜色变化分解成几个简单的“波形”。球谐函数的阶数 ll和次数 m决定了描述颜色的细节。例如,低阶球谐函数可以描述大的颜色变化(如球面上的颜色渐变),而高阶球谐函数可以描述小的、细微的颜色变化(如高光或反射细节)。通过一些数学公式(通常是积分)来计算球谐系数 \(c_l^m\)。这些系数告诉每个球谐函数对颜色的贡献。这相当于是泰勒展开:一个椭球上的颜色变化用一个函数很难写出来,我就用多个频率不同的函数去表达,然后记录的是各自函数的表达式与各自函数对应的权重。
计算球谐系数的公式:\(c_{l}^{m} = \int_{0}^{2\pi} \int_{0}^{\pi} C(\theta, \phi) \, Y_{l}^{m*}(\theta, \phi) \, \sin \theta \, d\theta \, d\phi\)
其中,球谐公式\(Y_{l}^{m}(\theta, \phi)\)的实数形式: 用球谐系数计算表达最后颜色:\(C(\theta, \phi) \approx \sum_{l=0}^{L} \sum_{m=-l}^{l} c_{l}^{m} Y_{l}^{m}(\theta, \phi)\)
用\(C(\theta, \phi)\)上查阅xyz坐标就能得到RGB值,因此这种类似于“5D函数”的东西终于表达出来了。论文中,\(l=4\),因此一共有1+3+5+7 = 16个球谐基函数,而RGB每一个通道都有一个\(C(\theta, \phi)\),因此关于颜色的表达将会使用3*16 = 48个参数(当然所有的3D高斯椭球共用一套球谐基函数)
Tile-Rasterization & α-Rendering
有了一堆的高斯椭球,我还知道一条光线视角下穿过点的opacity与RGB,如何综合它们得到一个最终的RGB值呢?论文中没有使用NeRF的density那一套逐pixel的公式,而是使用了逐tile(瓦片)的Alpha Rendering。
我们的方法首先将屏幕划分为 16×16 的瓦片,然后对 3D 高斯点进行视锥体和每个瓦片的剔除。具体来说,我们只保留那些在视锥体中具有 99% 置信区间的高斯点。此外,我们使用一个保护带来简化地剔除那些位置极端的高斯点(即那些均值接近近裁剪面并且远离视锥体的点),因为计算它们的投影 2D 协方差可能会不稳定。然后,我们根据每个高斯点与瓦片的重叠数量实例化每个高斯点,并为每个实例分配一个结合了视空间深度和瓦片 ID 的键。接着,我们使用快速的 GPU 基数排序(Radix Sort)对高斯点进行排序。注意,没有额外的每像素排序,而是根据这种初始排序进行混合。因此,我们的 α-blending 在某些配置下可能是近似的。然而,当高斯点的尺寸接近单个像素时,这些近似变得微不足道。我们发现,这种选择极大地提高了训练和渲染性能,同时在收敛场景中没有产生明显的伪影。
排序后,我们为每个瓦片生成一个列表,通过确定第一个和最后一个按深度排序的条目,这些条目投影到给定的瓦片上。对于光栅化,我们为每个瓦片启动一个线程块。每个块首先协作地将高斯点包加载到共享内存中,然后,对于每个像素,按前到后遍历列表,累积颜色和 α 值,从而最大化数据加载/共享和处理的并行性。当像素的 α 达到目标饱和度时,相应的线程停止。定期查询瓦片中的线程,当所有像素的 α 饱和(即 α 达到 1)时,整个瓦片的处理终止。
在光栅化过程中,α 的饱和度是唯一的停止标准。与之前的工作不同,我们不限制接收梯度更新的混合原语的数量。我们强制执行这一属性,以便我们的方法能够处理具有任意深度复杂性的场景,并准确学习这些场景,而无需进行场景特定的超参数调优。在反向传播过程中,我们必须恢复前向传播中每个像素的完整混合点序列。一种解决方案是将任意长的混合点列表存储在全局内存中。为了避免动态内存管理的开销,我们选择再次遍历每个瓦片的列表;我们可以重用前向传播中的高斯点排序数组和瓦片范围。为了方便梯度计算,我们现在从后向前遍历这些列表。
Pipeline
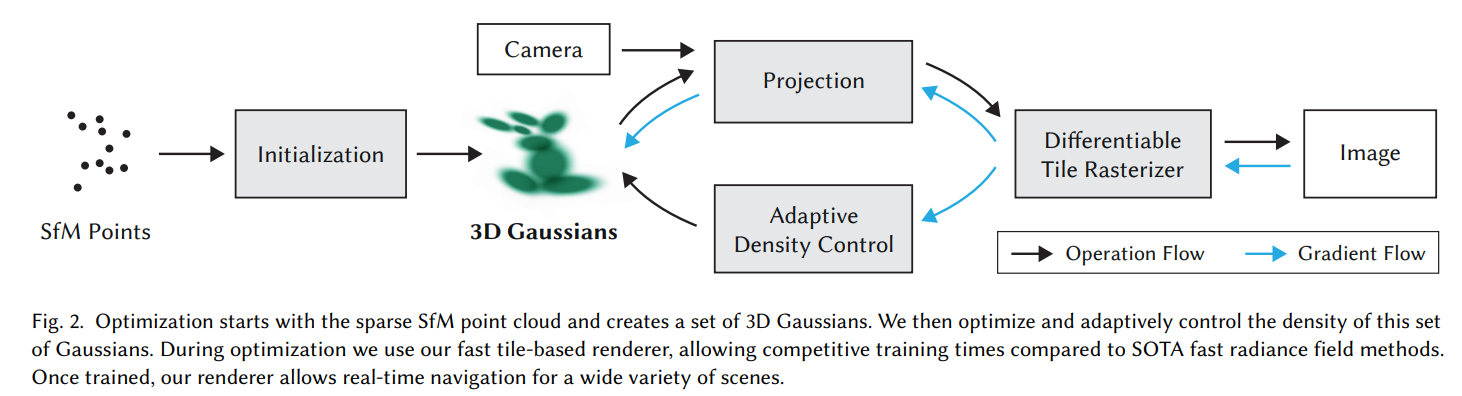
见上图。网络输入为一堆的照片以及对应的相机方向与位置,首先通过SfV(Structure from Motion)方法拟合出三维空间中的一系列点,然后各自为中心点初始化高斯椭球,包括它们的球谐系数,opacity,以及s向量(负责scale)与四元数q(负责旋转)。然后根据这个三维场景在一个摄像机视角下进行投影,然后用可微分tile-rasterizer进行光栅化成像,得到image,然后与ground truth进行比较算出loss,然后反向传播,更新Rasterizer, Projection, 3D Gaussians参数。
Loss为两张图片的\(L1\ Loss\) 与\(D-SSIM\ Loss\)(Structural Similarity Index Measure)的结合: 基于梯度自适应改变点云分布方式(Adaptive Density Control):在每隔一定epoch数量之后进行一次,决定是否更新点云的分布。第一种是Pruning,减少伪影的出现:其中不透明底低于阈值的,或者离相机太近的会被删掉。
第二种是Densification,过度重构或欠采样(这一部分就会基于梯度来进行判断)。有的时候,高斯椭球会不会过少或过多?当然有可能,如果完全依赖初始化的点云,那么就有些不合适了。如下图:两个
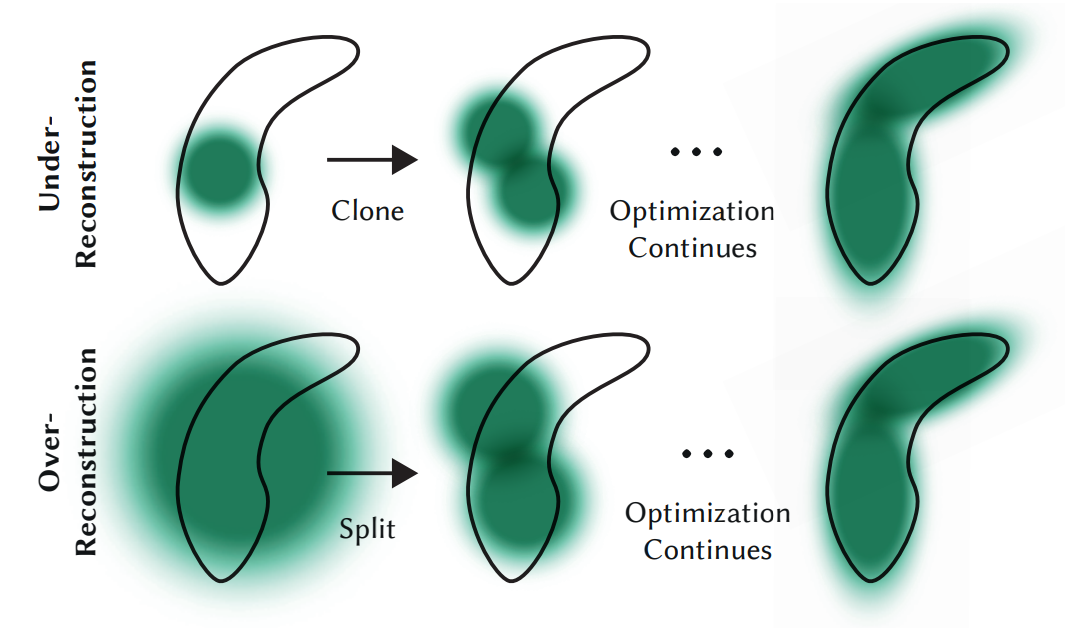
对于上下两个原来的高斯椭球来说,它们的梯度无疑是很大的。那么这个时候就判断这个高斯椭球的方差:如果过小,就说明是第一行的情况,需要clone出另外一个高斯椭球帮忙进行拟合;如果过小,说明是第二种情况,需要这个大高斯椭球分裂成两个小的,从而更好地拟合。
那么上述就是3D高斯泼溅的大致流程了。下面是关于它的伪代码图(source link):
