CNN
Innovation
假设一个visual recognition的任务,输入是200*200的RGB照片,那么考虑一个简单的全连接层,那么可想而知参数量非常的恐怖。同时:假设图片中的目标物体便宜了一小点,那么可想而知的是应该识别出的物体类别依然是一样的,这意味着目标物体在图像中应该有一种特殊的2D拓扑性质。
所以直觉上,我们希望一个新的神经网络来:
- 处理高维输入
- 充分利用图像中像素的2D拓扑性质
- 能够不收图像微小变化的影响(如微小的平移、变形等)
于是CNN就很好的利用了这些思想:注重于:
- local connectivity
- parameter sharing
- pooling/subsampling hidden units
Overview
First idea: Use a local connectivity of hidden units
Second idea: Share weights across certain units
Third idea: pool hidden units in the same neighborhood
Robust toward small deformations in object shapes by ignoring details
Fourth idea: Interleaving feature extraction and pooling operations
Extracting abstract, compositional features for representing semantic object classes
Methodology
Kernel是CNN的主角:一个kernel里面参数的和应该是1,这个卷积核会和图像进行卷积操作。一个平均数填充的卷积核所处理的结果是模糊化,仅是中间为1的卷积核的处理结果就是图像本身。
细节:卷积结果中计算完了所有的点积之后,还有偏置项
一个卷积核的大小是三维的,通常表示为(高度,宽度,通道数)。其中,高度和宽度是卷积核在空间上的尺寸,而通道数必须与输入张量的通道数相匹配。
有多少种这样的卷积核,输出的张量的通道数量就是多少。每个卷积核都会在输入张量上滑动并计算点积,产生一个输出通道。因此,如果有多个卷积核,每个卷积核都会产生一个独立的输出通道,这些输出通道组合在一起形成输出张量。
例如,如果输入张量的大小是(32, 32, 3),即32x32的图像有3个通道,而我们使用了16个卷积核,每个卷积核的大小是(5, 5, 3),那么输出张量的大小将是(28, 28, 16),其中28x28是输出图像的空间尺寸(取决于卷积核的大小和步长),16是输出通道的数量,对应于16个卷积核。
滑动(stride)与padding也是CNN中重要的概念:
滑动(stride)是指卷积核在输入张量上移动的步长。具体来说,它决定了卷积核每次移动的像素数。例如,如果stride为1,则卷积核每次移动一个像素;如果stride为2,则卷积核每次移动两个像素。
- 控制输出尺寸:stride越大,输出张量的空间尺寸(高度和宽度)越小。
- 控制特征提取的密度:stride越小,特征提取越密集;stride越大,特征提取越稀疏。

填充(padding)是指在输入张量的边缘添加额外的像素(通常是零)。填充的目的是控制卷积操作的输出尺寸,或者保持输入和输出的尺寸一致。
- 保持尺寸:通过添加填充,可以使输出张量的尺寸与输入张量的尺寸相同,或者接近输入张量的尺寸。
- 增加边界信息:填充可以减少边界像素的丢失,使卷积操作能够更好地处理图像的边缘信息。


感受野:其实就是卷积核的size
Closer look at activation function
一些常见的激活函数有:
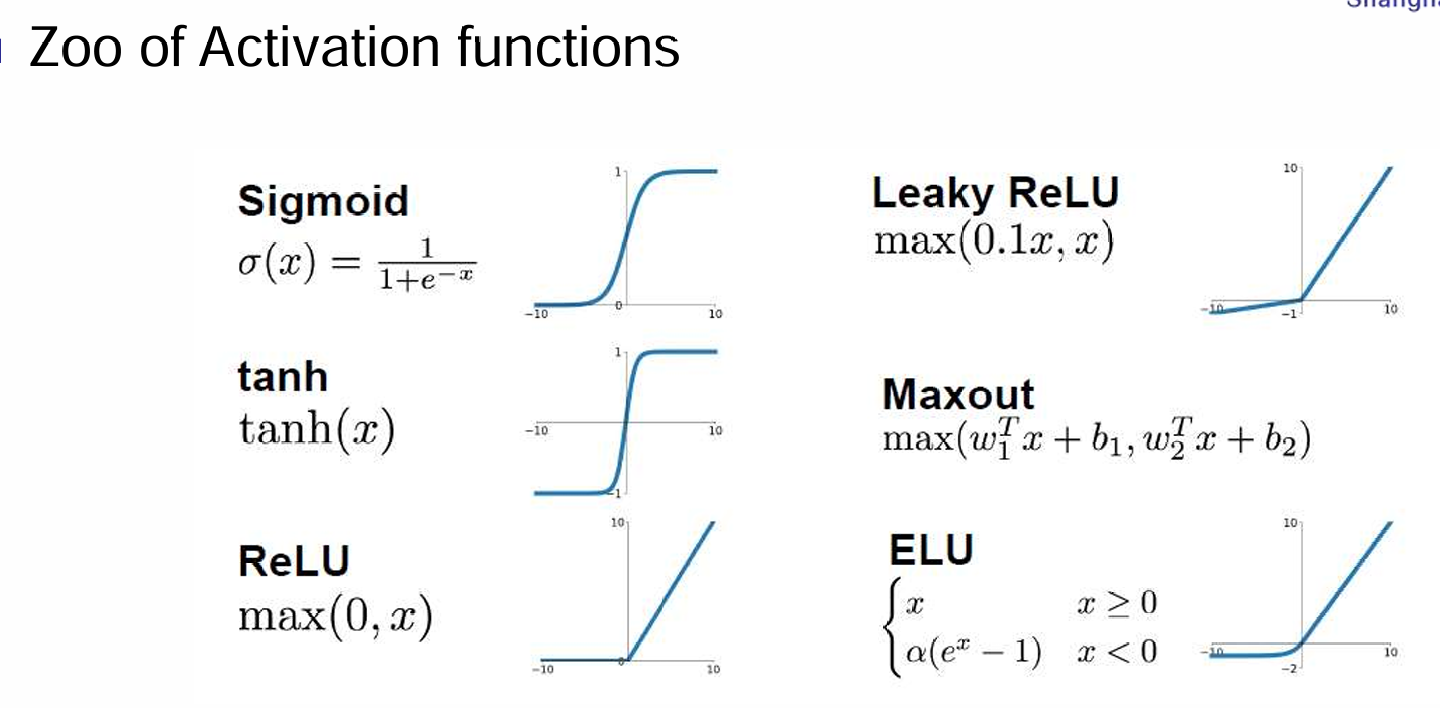
这些激活函数都能起到引入非线性性的作用。那么激活函数之间亦有差异吗?答案是肯定的。
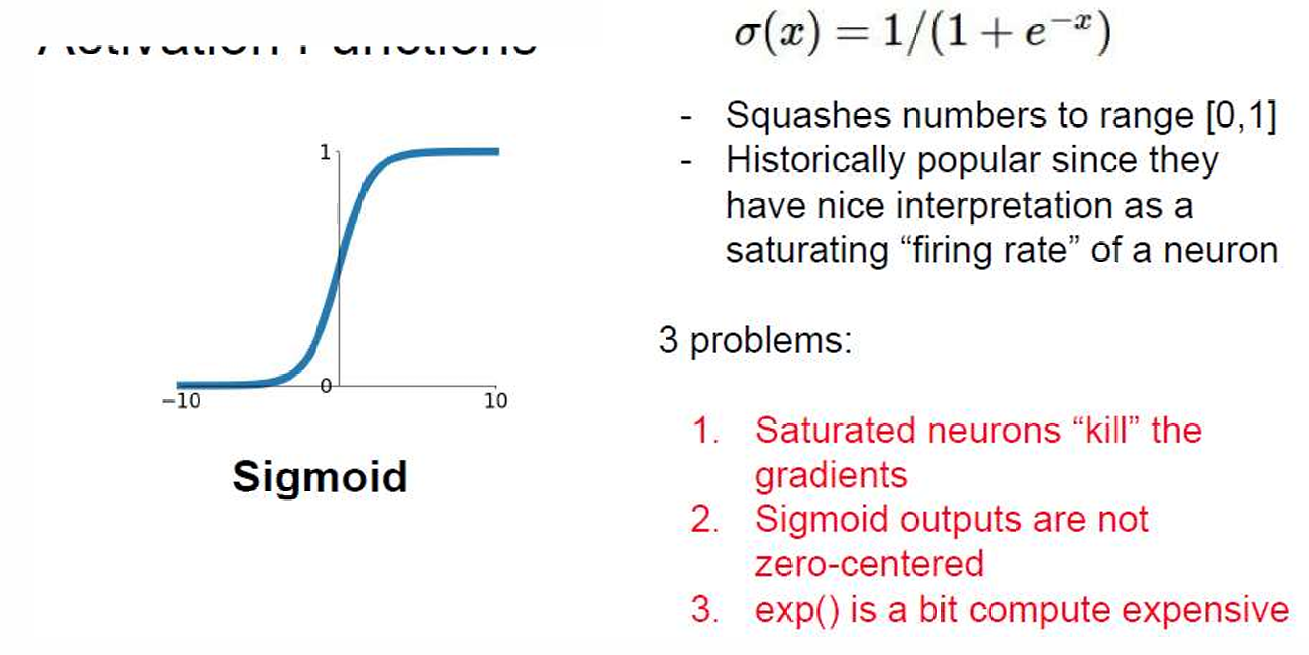
sigmoid是最为著名的,最终的输出值范围在0-1之间。历史上非常流行,因为它的输出可以被解释为神经元的激活概率或“发射率”(firing rate)。
缺点:
- 梯度消失问题:当输入值非常大或非常小时,函数的梯度接近于0,这会导致在反向传播过程中梯度消失,影响网络的训练效率。
- 非零中心化输出:Sigmoid 函数的输出不是以0为中心的,这可能会影响网络的训练速度和效果。、
tanh输出范围是-1到1,而且是中心对称的,这很好,但是依然在输入值很大或很小的时候,梯度非常的小。
ReLU函数避免了梯度消失的问题,而且计算效率非常高,在实践中收敛速度更快,并且在生物学角度上是更有可能的。但是也有缺点。首先是非零点中心化输出,其次就是输入如果小于0,那么意味着这些神经元不会被激活,那么就是死亡ReLU的问题。
Leaky ReLU就是为了防止死亡ReLU的现象,让负数阶段也有斜率,并且继承了ReLU的优点。

Pooling Layer
Reducing the spatial size of the feature maps:
-
Smaller representations
-
On each activation map independently
-
Low resolution means fewer details

Math Properties of CNN
首先是equivariance:等变性指的是当输入经过某个变换后,输出会以相应的方式变换,保持变换的一致性。具体来说,如果输入经过一个变换 g,那么输出应该是与变换相对应的输出变换。
数学表达式:对于每个输入 x,如果应用变换 g 到输入上,那么输出 \(\phi(gx)\) 应该等同于将变换 ggg 应用到输出上,即: $$ \exists M_g : \mathbb{R}^d \to \mathbb{R}^d \quad \text{such that} \quad \forall x \in \mathcal{X}: \phi(gx) \approx M_g \phi(x)
$$ 卷积操作本身就具有等变性。具体来说,卷积操作对于输入的平移具有等变性。如果输入图像中的某个特征(例如物体)平移了,那么卷积操作的输出也会相应地平移。也就是说,卷积对输入图像的平移不会改变其特征,只是位置发生了变化。
其次是不变性:不变性指的是当输入经过某个变换时,输出不会发生变化。也就是说,变换对输出没有任何影响。
数学表达式:对于每个输入 x,如果应用变换 g 到输入上,那么输出\(\phi(gx)\) 应该等于 \(\phi(x)\),即输出保持不变: $$ \forall x \in \mathcal{X}: \phi(gx) \approx \phi(x)
$$