Supervised Learning
监督学习已经是十分的熟悉了:要学习一个目标函数,输入的是训练集,最终要求的是输出一个近似拟合的函数,要求尽可能的接近目标函数。监督学习由下游任务的不同而进一步的分类:分类,回归(输出的是实数),以及结构化输出(structured output)
此处仅介绍naive bayes approach,关于分类任务的perceptron approach,regression及其loss function and regularization在182中有所讲解。
Unsupervised Learning也将略过,因为是182中的K-Means and Gaussian Mixture Model with EM steps
Classification
分类任务是非常常见的,比如说span email classifier,比如手写数字识别,比如物体识别分类。那么如何建模一个分类器呢?
Naive Bayes Classifier
一种model-based approach是设计一个模型(比如说贝叶斯网络),数据的label and feature都视作随机变量,然后对每一个观察到的feature进行实例化,最后根据features来query label's distribution。这是经典的建模思想。但是问题在于:如果是这样,贝叶斯网络的结果如何?我们如何学习参数?这几乎是下至传统人工智能上至高级机器学习的终极问题。
一种非常简单的例子如下:

将图片中的每一个像素都看成是一个feature,进一步地,看成一个随机变量,那么在这些像素组成的那么多随机变量的condition下,我们想知道label random variable Y的条件分布是怎样的。根据贝叶斯,我们知道这个分布是正比于Y的分布和在对应Y下Feature这些随机变量的条件联合分布的乘积的。那么问题就来了:我们应该学什么?我们需要明确:label and feature之间的关系是什么,并且进一步表示这个关系。如果feature之间条件独立(至少在我们认为的inductive bias下是),那么表现形式可以是条件概率分布。
如果有了这些关系的条件概率,那么inference就十分明确了,流程如下:
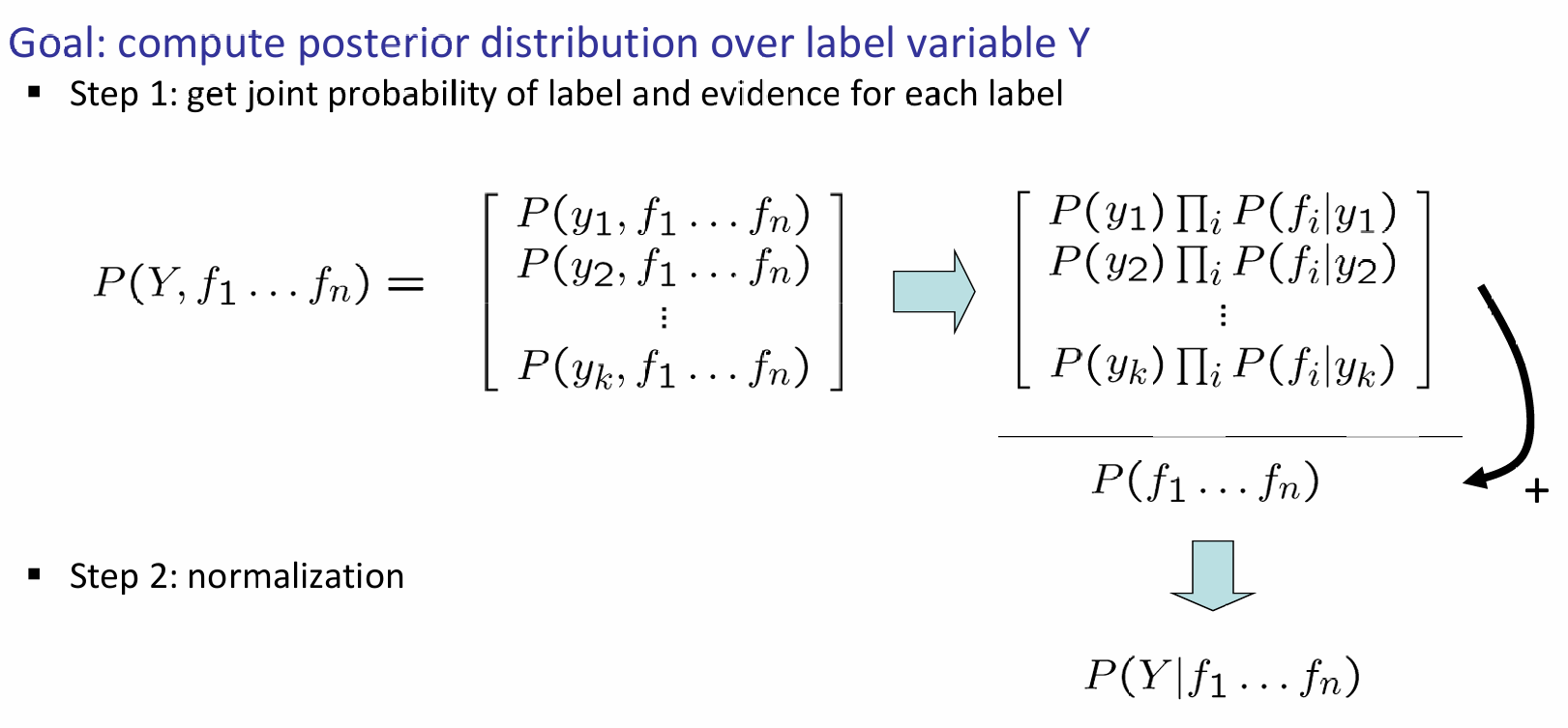
如果考虑诈骗邮件分辨的情景,那么核心参数就是label下每一个单词出现的概率了。这样是不是有点奇怪,那岂不是丢失了单词的order信息吗?没错,所以这种方式叫做'bag of words' approach。那么这个条件概率分布应该怎么学到呢?当然是得从数据集里面学了。一种很简单的方法是:在对应label下,该feature是否出现,在数据集上对这个进行统计,那么就能得到一个近似的条件概率。比如说这个情境中,1000个诈骗邮件中有50封出现了money单词,因此我们认为:在是诈骗邮件的背景下,出现money单词的概率是0.05.或者更专业地,可以考虑最大化似然来算出条件概率,而不是简单的看出现频率。
Laplace Smoothing
Laplace Smoothing(拉普拉斯平滑)是一种用于处理概率估计中的零概率问题的技术,特别是在朴素贝叶斯分类器中。当某个特征值在训练数据中没有出现时,直接使用经验频率会导致某些概率估计为零,这可能会影响模型的性能。Laplace Smoothing通过添加一个很小的常数(通常为1)来避免这种情况,从而确保所有概率都是正的。
原理
Laplace Smoothing的基本思想是为每个可能的特征值添加一个计数,即使它在训练数据中没有出现。这样做可以确保即使某个特征值在训练集中没有出现,其条件概率也不会是零。
公式
对于特征 f 和类别 y,Laplace Smoothing后的条件概率估计为:
\(P(f∣y)=count(y)+Vcount(f,y)+1\)
其中:
- count(f,y)是特征 f 在类别 y 中出现的次数。
- count(y)是类别 y 在训练数据中出现的次数。
- V 是特征 f 可能取值的总数。
应用
在朴素贝叶斯分类器中,Laplace Smoothing通常用于计算每个特征在给定类别下的条件概率。例如,如果我们有一个文本分类问题,其中特征是单词,类别是文档的主题,我们可以使用Laplace Smoothing来估计在给定主题下某个单词出现的概率。
优点
- 避免零概率:通过添加一个小的常数,Laplace Smoothing确保了所有概率都是正的,从而避免了零概率问题。
- 简单易用:实现简单,计算效率高。
缺点
- 平滑参数选择:虽然通常使用1作为平滑参数,但这个选择可能不是最优的,不同的问题可能需要不同的平滑参数。
- 过度平滑:在某些情况下,添加的计数可能过多,导致模型对训练数据过度敏感,从而影响泛化能力。
总的来说,Laplace Smoothing是一种简单有效的技术,用于处理概率估计中的零概率问题,特别是在朴素贝叶斯分类器中。然而,它也有其局限性,可能需要根据具体问题进行调整。
在条件和特征的取值空间都很大的时候,这种方法表现不佳,因此有线性插值这种新的方式:
